En espagnol
Francisco
García (avec Mathematica)
En anglais
Dirk Danckaert
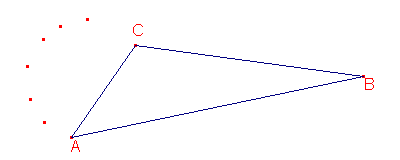
Après avoir déterminé quelques points approchés, on peut voir que la solution est un cercle qui passe par deux sommets du triangle.

Alors, je trace la médiatrice
du côté, je met un point sur elle, et construis un cercle
par les deux sommets. Puis je déplace le centre pour que le symétrico-latéral
d'un de ces points soit aproximativement rectangle.
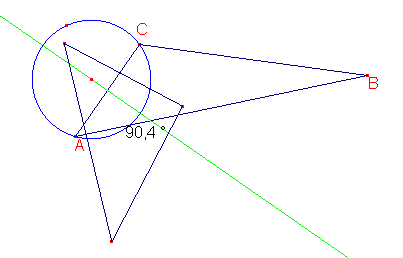
En cherchant de rélations avec le triangle, je vois que l'angle formé par le centre du cercle et le côté semble être le même que l'angle opposé du triangle.
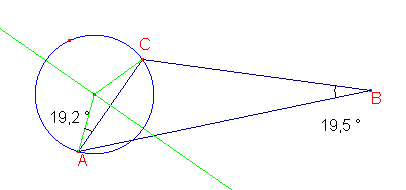
Alors, je fais la rotation de la droite AC autour de A avec l'angle ABC, et l'intersection de cette droite avec la médiatrice de AC. Le cercle qui a son centre à cette intersection et passe par A est un cercle solution.
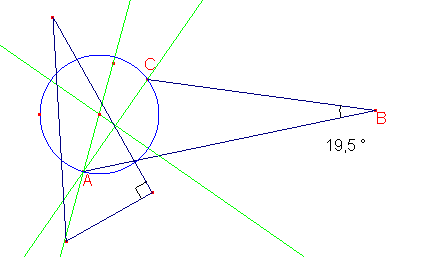
Tout d'abord, j'ai construit un triangle
rectangle ADE et j'ai trouvé que si P est sur la droite de l'hypotenuse,
son symétrico-latéral est rectangle.
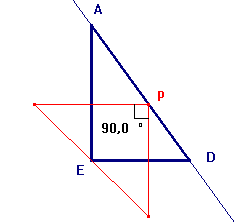
Alors j'ai pensé que ceci
devrait être vrai pour les autres triangles, que P doit être
sur une droite.
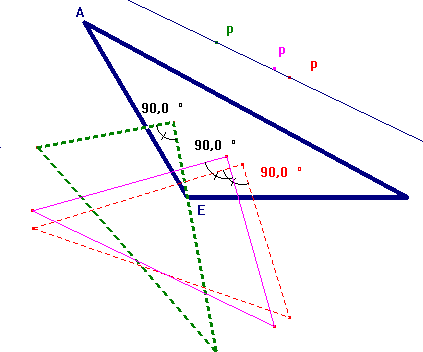
Ensuite Pablo m'a dit que quelques points étaient sur le cercle inscrit, ce qui contredisait mon hipothèse.
Nous avons décidé de construire un triangle quelconque et vérifier nos hipothèses.
Les trois premier points semblaient
être collinéaires, ce qui confirmait l'hypothèse de
la droite, alors nous avons construit d'autrres points pour la confirmer.
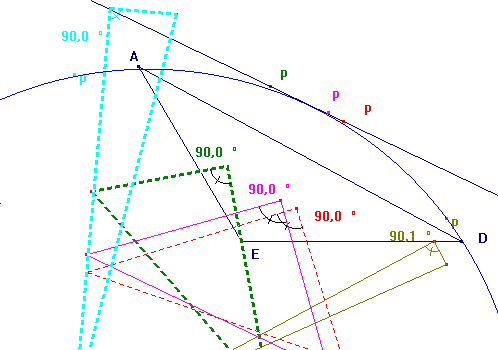
A notre surprise, les points n'étaient
pas sur une droite, mais semblaient être sur un cercle.
Alors, nous avons décidé
de recommencer avec un triangle plus petit.
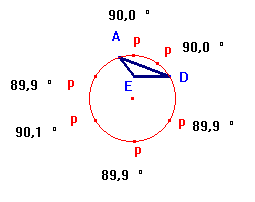
Nous avons construit un cercle quelconque
et nous l'avons ajusté pour qu'il passe par les points trouvés.
Nous étions convaincus pour le cercle, il restait à le construire
exactement.
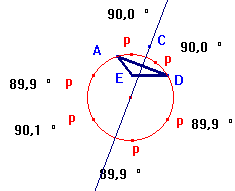
Nous avons construir le centre C
du cercle circonscrit de ADE , et nous avons constaté que la droite
perpendiculaire a AD par C passait aussi par le centre du cercle solution.
Mais où exactement?
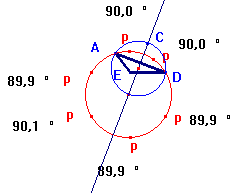
Ensuite nous avons construit le
milieu de C et le centre du cercle solution et nous avons cherché
une relation avec les points remarquables du triangle, sans succès.
Alors nous avons construit un cercle avec ce milieu comme centre et par
un sommet, et nous avons vu qu'il passait par C.
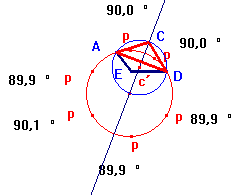
Alors, nous avons construit le triangle
ADC et son cercle circonscrit avec centre C'.
Ainsi, la solution est le cercle
de centre C' qui passe par A.
La solution complète du problème est constituée de trois cercles de centres K1, K2 et K3 Intersections des médiatrices de ABC avec les droites qui passent par le point de Lemoine et les sommets. Ces cercles passent par les sommets du triangle.
PROCEDE UTILISE
1 – J'ai construit un triangle quelconque ABC et un point P.
2 – J'ai construit A’ et B’ symétriques de P par rapport à AB et AC et j'ai tracé le segment A’B’
3 – J'ai construit une droite perpendiculaire au segment A’B’ par B’ .
4 – Ensuite C’symétrique de P par rapport à BC.
Alors, on aura une solution lorsque C' est sur la droite perpendiculaire à A’B’. J'ai obtenu ainsi quelques points approchés.
J'ai vérifié que ces solutions n'étaient pas allignées et j'ai pensé à un arc de cercle.
A fin de déterminer le "possible cercle", j'ai tracé des segment entre les points solution, et les médiatrices de ces segments. Elles semblaient être concurrentes.
Ensuite, j'ai fait le processus à l'inverse :
1 - J'ai construit ABC, la médiatrice de AB et un point K sur elle.
2 – Un cercle de centre K et rayon quelconque et un point P sur lui.
3 – Le triangle symétrico-latéral de P. J'ai déplacé K et le cercle pour obtenir des triangles rectangles.
4 – J'ai découvert que le cercle solution devait passer par A et B.
5 – J'ai fait plusieurs éssais pour trouver la position exacte de K, jusqu'à trouver qu'il est l'intersection de la médiatrice et la droite qui passe par le sommet opposé et le point de Lemoine.
je fais la construction du triangle, choisi un angle au hasard, le mesure,
et déplace le point libre M jusqu’à ce que cet angle devienne
égal à 90°.
je pointe la position ;
je réitère ces pointés pour de nouvelles positions
de M et constate que le lieu ressemble à un cercle passant par deux
points du triangle de départ
j’en conclue que le lieu est certainement constitué de trois cercles, chacun passant par deux sommets du triangle de départ
je place des points courants sur les trois médiatrices du triangle
de départ, construit les trois cercles passant chacun par l’un de
ces points et deux points du triangle ;
j’ajuste les positons des points courants de façon à
ce que le triangle construit par symétrie possède chaque
fois un angle droit (contrôle par mesure) ;
le codage des couleurs me permet de mieux me repérer
en construisant le triangle des centres des trois cercles, je constate, à vue, que les supports de ces côtés passent par les sommets du triangle de départ
étape infructueuse
je trace les cercles qui passent par M et deux sommets du triangle
construit
rien de particulier, mais j’ai toutefois construit le cercle circonscrit
au triangle de départ qui va me donner la solution…
je reprends l’idée de Sol2, trouve une méthode pour déduire deux lieux à partir du premier et puis, en traçant les supports des côtés du triangle gris, passant par les centres des cercles-lieux je constate, à vue, qu’ils sont tangents au cercle circonscrit au triangle de départ : j’ai ma solution
voilà une solution :
cercle circonscrit au triangle de départ
tangentes au cercle aux sommets du triangle
ces tangentes se coupent deux à deux suivant les centres des
cercles-lieux
ces cercles passent chacun par deux points du triangle de départ
j’ai complété le rectangle dont le triangle construit est une moitié et ai constaté que le lieu du 4e sommet est un cercle concentrique au cercle-lieu correspondant…