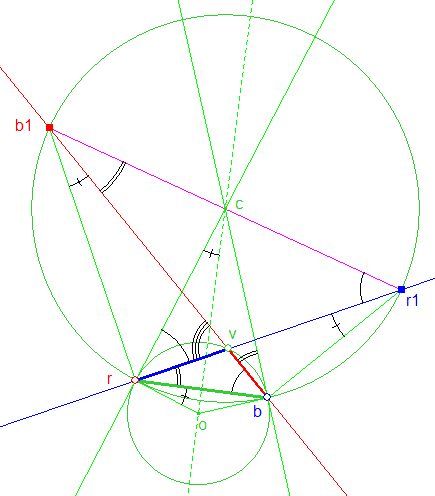
A) Montrons tout d’abord que les points b1 et r1 intersections de bv et rv avec le cercle (c) sont diamétralement opposés.

Appelons 1 l’angle du triangle rvb en b et 2 l’angle en r (angles représentés par un arc de cercle simple et un arc double).

L’angle extérieur en v, représenté par un arc de cercle triple, est appelé 3.

3 = 1 + 2 (1)

L’angle formé par br et le rayon du cercle circonscrit à rvb, passant par r est appelé 4 (il est représenté par un arc de cercle barré).

1 + 2 + 4 = p/2 (2)

Des relations (1) et (2) on déduit que 3 et 4 sont complémentaires.

Dans le cercle (c) les angles inscrits orb, soit 4, et rb1v interceptent le même arc ; ils sont donc égaux.

De même les angles brr1 et bb1r1, égaux à 2, et rbb1 et rr1b1, égaux à 1

Dans le triangle rr1b1, les angles b1 et r1 sont complémentaires :

r1 + b1 = 1 + (2 + 4) = p/2 d’après (2).

Le triangle rr1b1 est donc rectangle en r, et b1 et r1 sont diamétralement opposés sur le cercle (c).

B) Montrons enfin que le triangle symétrico-latéral r’v’b’ est rectangle en v’.

Traçons les cercles de centres r et b et passant par M.

Appelons 1, 2, 3 les angles représentés par des arcs de cercle simple, double, triple.

Dans le cercle de centre r, l’angle inscrit b’v’M, soit 2, et l’angle au centre b’rM, soit 2x3, interceptent des arcs complémentaires ; on en déduit :

2 = p – 3 (1)

Dans le cercle de centre b, l’angle inscrit Mv’r’, soit 1, et l’angle au centre Mbr’ interceptent le même arc, d’où

Mbb1 = 1 (2)

Dans le cercle de centre c, les angles inscrits Mrr1 et Mb1r1 interceptent des arcs complémentaires, donc
 
 

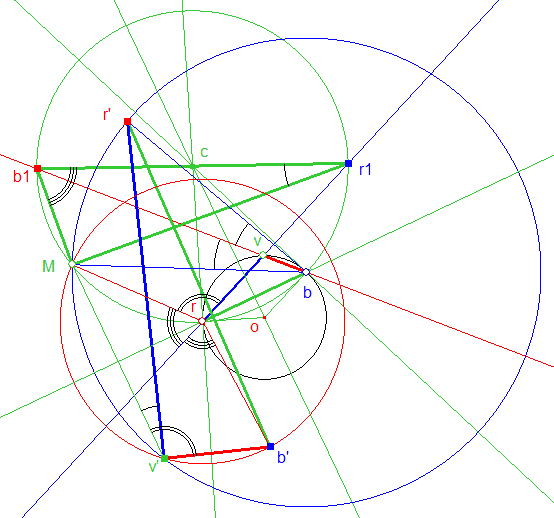
Mb1r1 = p – 2 = 3 , d’après (1)

Dans le cercle de centre c, les angles inscrits Mr1b1 et Mbb1 interceptent le même arc, ce qui donne :

Mr1b1 = Mbb1 = 1 , d’après (2)

Dans le triangle Mb1r1, rectangle en M,

r1 + b1 = p / 2 = 3 + 1

1 = p / 2 -- 3 (3)

Enfin, dans le triangle symétrico-latéral,

b’v’r’ = 2 – 1 = p – 3 – p / 2 + 3 = p / 2 (C.Q.F.D.)

Remarques :

- Tous les cas de figure n’ont pas été étudiés (en particulier quand v’M est à l’intérieur de l’angle droit v’).

Mais la démonstration reste analogue…

- Il faudrait de plus étudier la réciproque (quand r’v’b’ est rectangle, alors M est sur un cercle …)