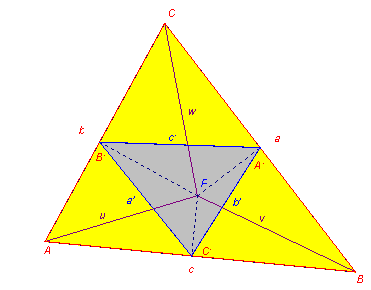
Properties of the symmetric-lateral triangle

I propose to rephrase the stated properties in terms of the pedal points of a point P. These are the orthogonal projections of P on the sides. The vertices of the symmetric-lateral triangle are the images of these pedal points under a dilation with factor 2.

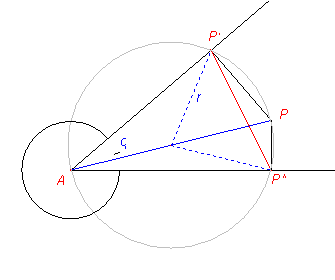
In the diagram above, P’ and P” are the projections on two lines through A, making an angle of . Since both angles AP’P and AP”P are right angles, A, P, P’ and P” lie on a circle with AP as a diameter. The distance between the pedal point P’ and P” is thus given by

This proves that, in any triangle, the distance between the pedal points of a given point P is proportional to the distance of P to the vertices of the triangle. This property allows an easy solution of several questions related to the symmetric-lateral or, equivalently, the pedal point triangle.

What’s the locus of P such that the pedal point triangle of P is right-angled in a? Applying Pythagoras’ theorem to the above diagram we find

The right hand side of this equation clearly represents a circle (think of introducing coordinates). The complete locus is the union of three such circles. Having proved that the locus is a circle, it is easy to construct it, as several people have already done. My solution is as follows: clearly P=B and P=C are points of the locus. Two other points can be found by constructing a perpendicular through B to the side AB. The intersection with AC gives another point P1 of the locus. Interchanging the roles of B and C gives a fourth point P2.. Observe that the angles P1BP2 and P2CP1 are right angles. This shows that P1P2 is a diameter of the circle.

What’s the locus of points P such that the pedal point triangle of P is isosceles? Proceeding in the same way as above, we find

which, again, is clearly a circle. Again, the complete locus is then the union of three such circles. Having proved that the locus is a circle I find some special points on it. It is clear that the vertex A belongs to the locus. It is also clear that the locus is symmetrical with respect to the side BC. So we have two points of the locus. Applying the sine-rule, we recast the condition above in the form

Now, it is well known that the angular bisectors in A divide the opposite side |BC| in just this proportion. So two other point of the locus are given by the intersections of the angular bisectors with the opposite side of the triangle. Since the bisectors cut each other in a right angle in A, also an element of the locus, these points define a diameter of the sought for circle.

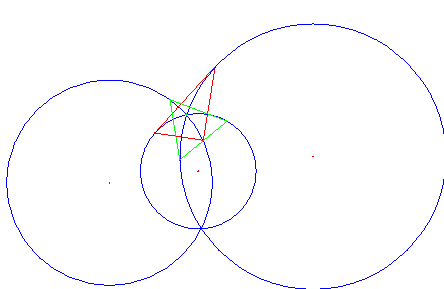
Finally, the three circles so constructed meet each other in a point P such that the pedal point triangle of P is equilateral. This solves the third problem.