1. Demostration d'un cas particulier:


Pour quoi si  APC=90-ABC, PaPbPc est rectangle?

J'ai commencé à déplacer P, et j'ai trouvé un cas spéciale dans lequel la construction se simplifie: lorsque P est sur la droite BC. Alors P=Pa.
J'ai construit les segments AP, APb et APc, qui sont égaux et forment des triangles isocèles. Dans cette configuration P, A et Pc sont alignés.



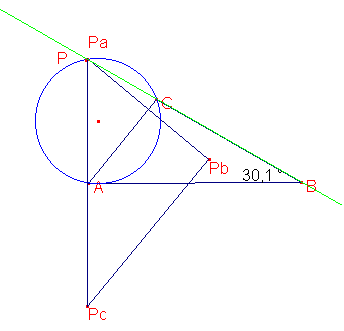
PPc étant perpendiculaire à AB, les triangles PAM (avec M projété de P sur AC) et  PPcPb sont semblables.En effet, par symétrie PPc=2PA et PPb=2PM. PMA étant rectangle, alors  PPbPc est rectangle aussi.

2. Démonstration générale:

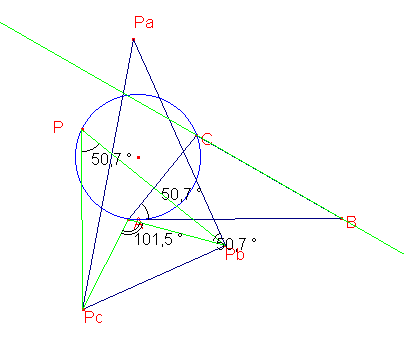
 Le triangle PcAPb étant isoscèle, les deux dernières égalités constituent une explication de pourquoi  PcPbPa est rectangle, car elles impliquent que PbPa est parallèle à la bissectrice de  PcAPb.

Je devais démontrer alors ces égalités.

En redéfinissant P comme point libre, j'ai trouvé que  PcPPb=CAB et PcAPb=2CAB étaient toujours vrais, mais  APbPa=CAB ne l'était plus.

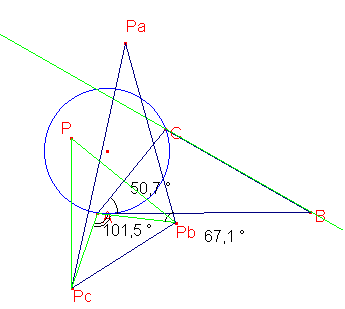
J'ai conclut que les deux premières égalités étaient dues à la symétrie, la troisième au fait que APC=90-ABC. Alors j'ai prit seulement les droites  AB et AC et le point P. En construisant les symétriques de  AP par rapport aux deux droites, j'ai prit conscience d'une composition de symétries axiales: AP est symétrique de APb et APc est symétrique de AP. Toute composition de symétries d'axes non parallèles étant une rotation du double de l'angle entre les axes, l'égalité  PcAPb=2CAB est démontrée.

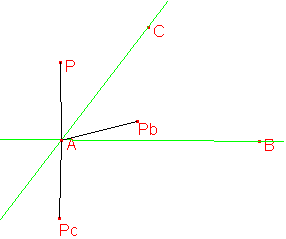
Alors, j'ai découvert une autre propriété invariante: APC-APbPa est constante.en observant la configuration, j'ai vu que cet angle était aussi PaPbC.

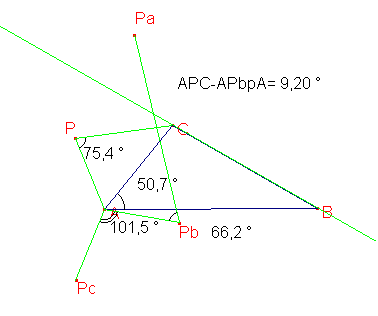
En considérant la symétrie de P par rapport à  BC, j'ai pu vérifier que PbCPa=2PCA+2PC(-B), c'est à dire que

PbCPa=2(180-BCA). PbPaC étant isoscèle, on peut calculer  PaPbC

PaPbC=(180-PbCPa)/2

= (180-2(180-BCA))/2

=(180-360+2BCA)/2

=(2BCA-180)/2

=BCA-90

Donc

APC-APbPa=PaPbC=BCA-90

Si APbPa = BAC, alors

APC=BCA-90+BAC

APC= BCA+BAC-90

APC=180-ABC-90

APC=90-ABC.