|
I. L'étude
de la corrélation entre variables
|
|
|
On travail sur un échantillon et on essaie
de tirer des conclusions pour la population dont il a été
tiré. |
|
Considérons un exemple dans lequel on tire
un échantillon composé de 50% de femmes et de 50% d'hommes
tous confrontés à trois tâches différentes A,
B et C. Les résultats indiquent que les femmes ont un bon score
pour A et les hommes pour B et C. Et on calcule le chi carré de
cet échantillon. Ensuite, il faut s'interroger sur l'origine des
résultats obtenus : les résultats de l'échantillon
peuvent être dus à deux sortes de facteurs, d'hypothèse:
1) ces résultats
sont dus au hasard de l'échantillonnage, c'est un résultat
aléatoire. C'est ainsi que l'on définit l' Hypothèse
nulle notée Ho.
2) ou bien ces résultats sont
systématiques, donc généralisables pour la population.
C'est ainsi que l'on définit l'Hypothèse alternative notée
H1. (Ho est unique, alors que H1 est multiple!!!!!!!!!!!!)
Il faut donc trancher entre ces deux hypothèses
et pour résoudre ce problème, on teste une hypothèse
: on commence toujours par considérer la première hypothèse,
l'hypothèse nulle Ho, la base de notre travail, qui stipule que
les résultats de l'échantillon ne sont pas généralisables
à la population, qu'ils sont dus à la distribution aléatoire
de l'échantillonnage. Si on reprend l'exemple ci-dessus, Ho stipulerait
que les femmes et les hommes auraient le même résultat pour
chaque tâche, il n'y aurait donc aucune différence entre sexe
dans la population.
Si Ho est rejetée, on se tourne alors
vers l'Hypothèse alternative, qui stipule que les résultats
de l'échantillons sont généralisables pour la population.
On teste Ho au moyen de la loi de la probabilité,
qui nous dit quelle est la probabilité d'obtenir le chi carré
calculé pour l'échantillon testé. Cette probabilité
vient du chi carré calculé pour un grand nombre d'échantillons
tirés dans une population et nous informe du risque d'erreur de
faire une généralisation abusive du résultat de l'échantillon.
Si la probabilité est faible, alors
le résultat n'est pas totalement compatible avec Ho et on considère
que le phénomène de l'échantillon existe pour l'ensemble
de la population. On peut ainsi conclure en affirmant que le résultat
de l'échantillon est SIGNIFICATIF à un seuil donné.
Si la probabilité est très grande,
alors on peut dire que le résultat de l'échantillon est dû
à un facteur aléatoire. Le résultat de l'échantillon
n'est donc pas incompatible avec Ho, mais on ne rejette ni Ho, ni H1. On
peut ainsi conclure en affirmant que le résultat de l'échantillon
est NON SIGNIFICATIF à un seuil donné. Il n'y a donc aucune
conclusion, car on ne peut jamais déterminer avec certitude si Ho
est vraie ou fausse. C'est seulement probable ou improbable de ne pas rejeter
Ho, car elle n'est pas contredite par les données. |
-
Distribution de l'échantillonnage
de la statistique de chi carré et la loi de chi carré :
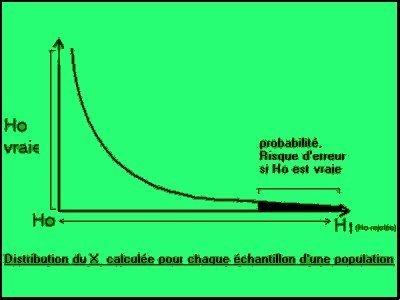
La loi de chi carré nous indique comment
se comporte la distribution de l'échantillonnage de la statistique
de chi carré si l'hypothèse nulle Ho est vraie, c'est-à-dire
lorsque le chi carré se rapproche de zéro.
Grâce à cette distribution, on
peut déterminer quelle est la proportion d'échantillons qui
se trouvent dans un zone du graphique suivant:
|
-
La démarche contient donc
4 étapes :
1)
On constitue l'échantillon d'une population et on étudie
certaines caractéristiques. Par exemple:
2 variables
2) On calcule un indice dont
la distribution d'échantillonnage est connue lorsque Ho est vraie.
Par exemple chi carré
3) On détermine la probabilité
d'obtenir une valeur au moins aussi élevée que la nôtre
à cause du hasard de l'échantillonnage.
4) On décide si oui ou
non on doit rejeter Ho et adopter H1. |
-
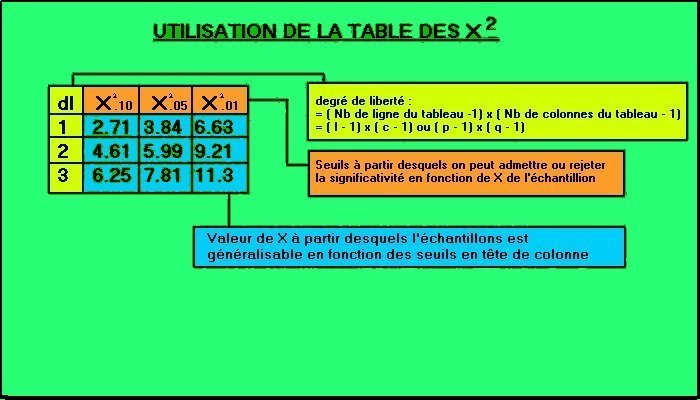
Utilisation de la table du chi carré
:
Pour décider du rejet ou non de Ho,
on utilise la loi binomiale qui va nous donner le risque d'erreur
au moyen d'une probabilité en consultant cette table.
Exemple :
On a un tableau de données dont les
dimensions sont les suivantes :2 lignes et 4 colonnes (2x4). Son degré
de liberté ((2-1)x(4-1)) est égal à 3. Si on consulte
la table de chi carré au niveau de la ligne "3" (dl=3) et de la
colonne "chi carré.05" (alpha.05 del a loi normale) on trouve la
valeur "7.81".
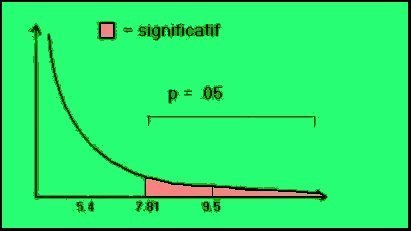
Si le chi carré de l'échantillon
est égal à 9.5 (>7.81) alors la probabilité (risque
d'erreur) <.05. On peut ainsi dire que le chi carré de l'échantillon
est significatif à .05.
Si le chi carré de l'échantillon
est égal à 5.4 (<7.81) alors la probabilité (risque
d'erreur) >.05. On peut ainsi dire que le chi carré de l'échantillon
est non significatif à .05
|
-
Critères d'appréciation
dans le calcul :
Plus le chi carré augmente, plus on a la
chance d'avoir un résultat significatif. Mais il est important de
préciser que la signification du chi carré de l'échantillon
dépend de deux éléments : -du chi carré de
l'échantillon
-du degré de liberté. |
-
Il y a deux catégories de
test :
1) Les test non paramétriques:
ils sont toujours applicables sans faire des hypothèses sur les
caractéristiques de la population. Ces tests sont appliqués
à des variables qualitatives telles que chi carré.
2) Les test paramétriques:
il faut toujours faire des hypothèses sur les paramètres
de la population. Ces tests sont applicables à des variables quantitatives
telles que r de Bravais-Pearson. |
-
La méthode du chi carré
:
1) Pour les tests d'hypothèses,
on utilise une loi de la probabilité, celle du chi carré,
car elle décrit le comportement du phénomène qui nous
intéresse dans certaines conditions :
-lorsqu'on
veut calculer le chi carré, les effectifs théoriques (n'ij)
doivent tous être plus grand ou égal à 5 afin de pouvoir
appliquer la méthode inférentielle. Mais on peut également
l'appliquer quand 25% des cellules du tableau des effectifs théoriques
ont un score plus petit que 5.
2) Si on travaille sur un tableau
de dimension 2x2 (2 lignes; 2 colonnes), la formule est un peu corrigée.
On utilise alors le chi carré de Yates qui donne un résultat
plus petit que celui du chi carré d'origine. La formule est la suivante
:
3) La distribution d'échantillonnage
de chi carré a une forme qui se modifie en fonction du
degré de liberté. Au fur et à mesure qu'il
augmente, elle converge avec la loi normale (dl=30). |
-
La méthode du r de Bravais-Pearson
:
Rappel: Le r nous informe sur la forme
de la relation (linéaire, non linéaire), sur son sens (positive,
négative) et sur son intensité (nulle, parfaite). On peut
également faire une représentation graphique sur un plan
cartésien qui nous donnera déjà des informations sur
la relation.
La méthode est identique à celle
du chi carré, mais elle s'applique aux variables quantitatives:
1) On commence avec une hypothèse
nulle Ho qu'on va mettre à l'épreuve et voir si on peut accepter
l'hypothèse alternative H1.
-L'hypothèse
nulle Ho implique que le r de la population serait égal à
zéro
-L'hypothèse
alternative H1 implique que le r de la population ne serait pas égal
à zéro.
2) La distribution d'échantillonnage,
lorsque Ho est vraie, est symétrique par rapport au zéro.
Elle dérive de la loi de Student.
La table de r: il s'agit de la même
méthode utilisée pour la table de chi carré mais seul
la façon de déterminer le degré de liberté
change.
La signification du r de l'échantillon:
La signification dépend de la valeur de r (plus r est grand, plus
il est significatif), de l'effectif n et du degré de liberté
dl.
-"r" est SIGNIFICATIF si la valeur absolue
du r de l'échantillon est plus grand ou égal à "r
alpha" trouvé dans la table, si la probabilité est plus petit
ou égale à la valeur de alpha.
-"r" est NON SIGNIFICATIF si la valeur absolue
du r de l'échantillon est plus petit que "r alpha" trouvé
dans la table, si la probabilité est plus grande que valeur de alpha.
L'intervalle de confiance: on le détermine
pour estimer le r existant dans la population. On applique la formule suivante
lorsque l'effectif de l'échantillon supérieur à 50
ou parfois à 100
Interprétation des résultats:
1) Si le r de l'échantillon
est SIGNIFICATIF, il est probable que la relation entre les deux variables
existe aussi pour la population. Cette relation est positive si r est positif,
elle est négative si r est positif.
2) Un résultat significatif
ne permet pas de savoir si la relation avec la population est de forte
ou de faible intensité. |
-
La méthode du Rho de Spearman
:
On procède de la même manière
que pour les deux méthodes précédentes, à la
différence près qu'on traite des variables ordinales.
Lorsqu'il y a deux distributions de rang à
comparer, on établit le classement de chaque personne pour chaque
épreuve et ensuite on calcule le rho.
Les hypothèses sont les suivantes:
-L'hypothèse nulle Ho implique que
le rho de la population serait égal à zéro
-L'hypothèse alternative H1 implique
que le rho de la population serait égal à 1.
Lorsque l'hypothèse nulle Ho est vraie
et que l'effectif de l'échantillon est plus grand ou égal
à 10, le rho se distribue selon la loi du r de Bravais -Pearson. |
|