[Next] [Previous] [Up] [Top]

chapitre 3 Modèles du décideur politique

3-2.2 Modèles de choix à rationalité limitée

En politique, contrairement aux situations expérimentales de la science cognitive, les problèmes sont très souvent présentés et discutés sous une forme déjà structurée. Ce qu'un chercheur peut observer de l'extérieur ne représente que très rarement le processus de décision en entier, mais plutôt l'argumentation pour un choix déterminé à prendre. Ainsi, le travail empirique de Saris et Gallhofer *1est fondé essentiellement sur l'argumentation de décideurs comme on la retrouve dans des transcriptions de décisions ou encore dans des textes officiels.

La plupart des modèles normatifs de choix sont fondés sur le modèle général de l'espérance subjective d'utilité (angl. "Subjective expected utility" (SEU), cf. Neumann and Morgenstern:47). Voici le principe de base du calcul de l'espérance subjective d'utilité: un décideur doit choisir la stratégie qui aura l'utilité espérée subjectivement la plus élevée. Un choix i peut conduire à plusieurs résultats ij. Le décideur calcule pour chaque résultat ij possible une probabilité d'occurrence ainsi qu'une utilité. L'utilité prévue d'un seul résultat devient le produit de son occurrence potentielle et de son utilité. En conséquence, la SEU d'une stratégie (ou d'un choix dans un exemple simple) est égale à la somme des SEU de tous les résultats possibles pour cette stratégie. Voici la formule pour le modèle simple:

SEU(stratégiei) = Somme(probabilitéij) * Utilité(résultatij)

Ce modèle normatif dont il existe des versions plus sophistiquées ayant par exemple des attributs multiples à juger pour chaque résultat, possède plusieurs défauts pour la description de la réalité empirique:

Examinons la structure d'un arbre simple de décision dans la figure 3-3. Il s'agit d'une action-réaction

. Le premier décideur possède deux choix d'actions et l'autre trois. En tout, il existe donc 6 résultats possibles. Cet arbre est légèrement plus complexe que celui d'un jeu comme le dilemme du prisonnier. Tout d'abord, les actions des décideurs se suivent. Ensuite, chaque action possible de l'autre ainsi que les résultats potentiels possèdent un coefficient de probabilité. Ce diagramme arborescent représente donc la séquence chronologique des actions mises à disposition du décideur et de l'autre acteur à un certain moment dans un processus de décision. Si l'on imagine que les chaînes d'action peuvent se prolonger et que plusieurs acteurs peuvent y participer, etc., on peut vite se rendre compte d'une explosion combinatoire des calculs à faire si l'on désirait appliquer le modèle SEU jusqu'au bout. Comme les recherches en intelligence artificielle l'ont montré, il est plus "rationnel" de simplifier ces arbres de décision pour arriver à une solution plus abordable en termes de ressources, mais qui reste néanmoins presque aussi efficace. Avant de discuter ces stratégies en détail, nous nous pencherons brièvement sur la question du codage de ces arbres, tels qu'ils sont présentés dans des "traces" textuelles.

Les arbres de décision

Il est relativement aisé de traduire l'argumentation d'une décision dans des structures arborescentes. Des tests effectués par les auteurs (Gallhofer and Saris 1979, et Saris and Gallhofer 1983) ont même montré qu'une très haute fiabilité inter-codeurs est obtenue*2. Un codeur doit effectuer les pas suivants: (cf. Gallhofer and Saris 1983:7, 1979:412-414)

  1. Lecture du texte

  2. Recherche des concepts de décision suivants:

  3. Actions mises à disposition du décideur

  4. Actions mises à disposition des autres

  5. Résultats potentiels pour le décideur

  6. Valeurs subjectives des résultats potentiels

  7. Probabilités subjectives pour les résultats potentiels

  8. Probabilités subjectives pour les actions des autres décideurs.

  9. Elaboration d'un arbre de décision en faisant la combinaison des éléments de l'argumentation.

Pour garantir un codage uniforme, les règles additionnelles suivantes doivent être également respectées.

  1. Si seule une alternative d'action est mentionnée explicitement mais que son résultat est exprimé sous forme probabiliste, son complément (la négation du résultat) doit être également représenté dans le diagramme.

  2. Si la probabilité d'un événement est égale à la certitude (il n'existe donc pas d'alternative), une branche seulement doit être mentionnée.

Nous avons traduit la structure de la décision

que l'on retrouve de façon informelle chez Gallhofer and Saris (1979:412-413) dans une grammaire générative*3 que l'on retrouve dans la figure 3-4 "Une grammaire pour la génération des arbres de décision" [p. 66]. En étudiant cette grammaire, nous voyons qu'au début d'un arbre de décision se trouve le PROBLEME du décideur, qui résulte au moins en une ACTION à disposition. Si l'on analyse cette grammaire depuis le "bas", on peut remarquer que chaque branche de l'arbre de décision doit aboutir à un résultat simple ou complexe décrit par une liste d'attributs. Il n'existe pas beaucoup de restrictions pour cette grammaire. Chaque ACTION peut directement en entraîner une autre du ressort de celle qui l'a déclenchée ou de l' "autre". Les deux types d'ACTIONS (les actions du décideur et celles des autres) peuvent conduire à des RESULTATS, qui sont exprimés par un couple résultat+valeur au moins. Si un résultat qui n'a pas été lié à une action a eu lieu, on le code comme NOUVEAU-DEVELOPPEMENT. Finalement, un résultat peut également engendrer des sous-résultats. En somme, on peut combiner presque tous les éléments avec tous les éléments de cette grammaire.

Cette souplesse correspond assez bien à celle de la perception qu'un décideur a de la réalité. Nous montrons l'eexemple d'un arbre de décision en indicant quelles règles ont été utilisées dans la figure 3-5 "Exemple d'un arbre de décision (selon Gallhofer et Saris 79)" [p. 67].

La nature des résultats et des probabilités est discutée plus loin plus en détail. Le problème avec la méthode de travail de Saris et Gallhofer est que le décideur omet souvent les éléments de décision dans son argumentation et ne les exprime que très rarement d'une façon précise. Parfois, il indique seulement des ordres de priorité, parfois il emploie uniquement des valeurs binaires comme "probable/improbable" et "bien/mauvais". Les arguments réellement utilisés sont donc souvent moins complexes que les possibilités offertes par notre grammaire. De plus, le décideur laisse volontiers aussi des branches improbables ou hautement indésirables en dehors de son arbre de décision.

Les problèmes des valeurs complexes avec incertitude

Les décisions politiques (en tout cas au plan analytique) sont très souvent d'une très grande complexité. Le décideur se trouve devant de multiples possibilités de choix, les résultats sont toujours probabilistes et représentent des aspects multiples qui devront être évaluées. Mais ceci ne signifie pas que les problèmes sont toujours formulés dans toute leur complexité par les décideurs (cf. Saris 83:1). Il existe un grand nombre de méthodes pour simplifier. Il y a plusieurs "méthodes" pour réduire la complexité des résultats, notamment les suivants:

Un exemple

peut illustrer ces trois méthodes: en Suisse, en 1960, plusieurs groupes sociaux et politiques auraient aimé instaurer un système pour contrôler, diminuer ou interdire l'acquisition d'immeubles par des étrangers*4. Par ailleurs, beaucoup de gens étaient opposés à toute limitation de la liberté du commerce. L'affaire a été portée devant le parlement fédéral et il a été proposé d'instituer une législation réglant la matière. Dans la discussion très animée qui s'est ensuivie, un grand nombre des dimensions du problème ainsi que d'éventuelles solutions ont été discutées. L'exemple de la stratégie d'un acte légal et l'évaluation des dimensions du résultat possible est montré dans la figure 3-6 "Un problème complexe avec incertitude: la création d'un acte légal" [p. 68].

Parmi les participants à la discussion au parlement, plusieurs façons de représenter le problème sont apparues. Toutefois proposants et opposants ont structuré leur argumentation selon certaines lignes principales. Les avocats d'une solution législative ont eu tendance à rendre le problème de l'acquisition des immeubles très important et croyaient au succès éventuel d'une législation en la matière. Dans leur argumentation, des effets secondaires négatifs ont été exclus par l'attribution ou d'une valeur négative très petite ou d'une valeur neutre ou encore d'une probabilité très basse. Les adversaires ont soit nié le problème (c'est-à-dire l'utilité de l'acte), soit attribué des valeurs très négatives aux effet secondaires. Cette discussion sommaire montre d'une façon exemplaire que le choix n'est qu'une composante parmi d'autres dans un processus de décision. La perception et la présentation du problème sont tout aussi importantes que les choix, si ce n'est plus importantes. On voit également très bien qu'un problème est mis en rapport avec une vision du monde. Donc parler du choix, sans parler de la vision du monde qui est derrière n'a pas beaucoup de sens, car on choisit (explicitement) seulement parmi les options qu'on se met soi-même à sa disposition ou qui sont imposées par d'autres participants au processus de décision. *5.

Le tableau dans la figure 3-6 n'est qu'un résumé de la discussion sur les résultats finaux d'une action. Or les arguments ont été présentés en plusieurs étapes et non pas en une seule fois comme cette figure pourrait le faire croire. C'est une stratégie courante pour simplifier un problème, comme on peut le montrer par exemple par le message du Conseil Fédéral au parlement au sujet de l'arrêté fédéral qu'il lui soumettait pour discussion:

(1) Le Conseil fédéral, après une brève présentation de l'historique des événements, fait part de sa perception du problème. Le Conseil fédéral justifie l'idée d'une restriction de l'acquisition d'immeubles par des étrangers avec de simples arguments binaires: notre économie sera affaiblie si rien n'est fait (problème principal). Des avertissements à des vendeurs suisses ont été ignorés (donc des instruments para-légaux ne fonctionnent pas). Des restrictions limitées sur des opérations immobilières étrangères sont justifiées si elles protègent le bien public (donc quelques effets secondaires doivent être acceptés). En somme, le problème est réduit au simple problème sans incertitude suivant: la valeur d'un acte légal est supérieure à la valeur d'une non-action.

(2) Une fois que cette réduction est acceptée comme valable (ce qui s'est produit), la discussion peut porter dans une deuxième étape sur les moyens légaux à employer. L'arbre de décision

dans la figure 3-7 donne une partie de l'argumentation: Les stratégies S1 à S3 sont exclues soit par manque d'efficacité (les résultats ont une valeur totale basse), soit par une valeur négative forte. La stratégie S4, c'est-à-dire un acte légal instaurant un régime d'approbation, est jugée préférable sous réserve de sa constitutionnalité et de sa conformité au droit international.

(3) Dans une troisième étape, la constitutionnalité et la conformité au droit international seront discutées. Comme il n'existe pas de tribunal constitutionnel, la constitutionnalité est une affaire politique en ce qui concerne les cas tangents. Pour contourner le problème du droit international, le parlement décidera d'associer les sujets (assujettis au régime) aux personnes ayant un domicile à l'étranger. Les étrangers habitant la Suisse seront associés aux Suisses. Cette solution a été déclarée la seule possible tout en ayant des effets secondaires négatifs qui ont d'ailleurs été corrigés dans une certaine mesure au niveau des ordonnances d'application de la loi.

Cet exemple montre bien que dès qu'un problème atteint une certaine complexité, il est traité en plusieurs étapes, chacune réduisant la complexité des choix à faire. Pour chacune de ces étapes, différentes règles de décision ont été utilisées. Ces règles s'utilisent selon la façon de présenter le problème, comme nous allons le voir maintenant.

L'utilisation de règles de décision

En règle générale, les décideurs ne mentionnent pas explicitement les règles de décision qu'ils emploient pour choisir entre des alternatives. Ils ne présentent que les faits et la solution (cf. Gallhofer 83:3-4). D'un côté, on retrouve donc une présentation des composantes du problème de décision, à savoir les stratégies (choix) à disposition, les résultats potentiels et les probabilités. L'évaluation des résultats se fait selon des règles opaques. Comment faire le lien entre la description d'un problème de décision et les choix opérés? Comment trouver la règle de décision? Lorsqu'il est impossible d'étudier un décideur dans des conditions cliniques ou dans un interview ex post facto, il faut procéder analytiquement comme Gallhofer et Saris l'ont fait dans leurs études.

Nous allons présenter brièvement les règles heuristiques de décision que ces auteurs ont inférées dans leurs études de décisions. Tout d'abord, on peut classer un problème de décision selon les dimensions (1) valeurs simples/complexes, (2) valeurs avec ou sans intensité, (3) incertitude avec ou sans intensité. En combinant ces dimensions, nous arrivons à huit types de problèmes. En accord avec la présentation du problème et de la solution prise par le décideur, on peut inférer qu'il a choisi l'une des règles de décision suivantes:

  1. "Subjective expected utility" (SEU) et SEU multi-attribut: choix de la stratégie qui offre l'utilité la plus élevée.

  2. Eviter le risque: choix de la stratégie qui offre la plus grande probabilité d'un résultat positif (ou encore la plus faible possibilité d'un résultat négatif). Les probabilités des résultats doivent être classées au moins sur une échelle ordinale. Les valeurs doivent être au moins classéesen positives ou négatives.

  3. Dominance: choix de la stratégie qui est meilleure que les autres par rapport à un aspect et au moins équivalente aux autres pour les autres aspects.

  4. Lexicographique: Il faut d'abord classer les aspects dans leur ordre d'importance, et ensuite prendre la meilleure stratégie pour l'attribut le plus important.

  5. Addition d'utilités: addition des valeurs de chaque attribut du résultat par stratégie et ensuite choix de la stratégie ayant la valeur totale la plus élevée. Il s'agit ici d'un calcul SEU sans incertitude.

  6. La règle de Simon (satisfycing): choix de la première stratégie qui promet un résultat satisfaisant, certains critères posés comme nécessaires.

  7. La règle de Simon renversée (negative satisfycing): exclusion de toutes les stratégies qui donnent un résultat négatif aussi longtemps qu'il existe une stratégie qui pourrait conduire à un résultat positif.

Les auteurs ont découvert qu'étant donné l'information sur les valeurs et les probabilités, le choix (et ainsi la règle de décision) peut facilement être prédit (Gallhofer 83:11). Ce constat apparaît surprenant, mais leurs recherches montrent que l'emploi des règles citées ci-dessus pour des problèmes simplifiés est en accord avec le modèle SEU. En ce qui concerne les problèmes avec des valeurs simples

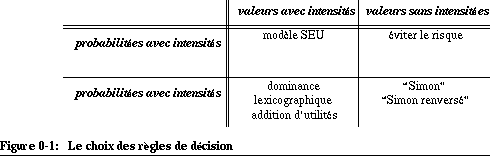
, la Figure 3-8: "Le choix des règles de décision" [p. 72], montre dans quelle situation quelle règle doit être choisie. En ce qui concerne les problèmes à résultats multi-attributs, ou les problèmes à étapes et résultats multiples, les décideurs utilisent des contraintes et des spécifications additionnelles qui dans beaucoup de cas garantissent également un résultat en accord avec le modèle SEU.

Les recherches de Saris et Gallhofer sur l'argumentation des décideurs complètent les travaux théoriques et cliniques d'autres chercheurs comme Huber (82) et Svenson (89a). Il est clair que les arguments présentés dans des situations de discours ou de discussion ne représentent pas forcément le processus de décision en son entier. Toutefois il permettent de faire des inférences importantes sur ces processus. En complétant ces informations avec d'autres (comme des résultats d'expériences cliniques, des entretiens en profondeur, etc.), on se rapproche de la structure des processus réels.

Les arbres de décision
Les problèmes des valeurs complexes avec incertitude
L'utilisation de règles de décision
THESE présentée par Daniel Schneider - 19 OCT 94

Generated with WebMaker