[Next] [Previous] [Up] [Top]

chapitre 3 Modèles du décideur politique

3-2.1 La théorie des jeux

La théorie des jeux est un outil mathématique développé principalement par John von Neumann à partir de 1920. Le premier ouvrage fondamental date de 1944 (Von Neuman et Morgenstern 47). Assez rapidement, cette théorie a été saluée comme une solution éventuelle aux problèmes de formalisation que connaissent les sciences sociales. Son champ d'application est l'acteur intentionnel et rationnel qui est en interaction avec au moins un autre acteur. Voici une définition de sa rationalité limitée: "Very generally, behaving rationally in game theory means acting to maximize the achievement of some postulated goal, where the outcome depends not only on chance events and "nature", but also on the actions of other players with sometimes cooperative and sometimes conflicting interests" (Brams 75:XV). La théorie des jeux sert donc surtout à modéliser des situations où des acteurs sociaux prennent des décisions individuelles séparées, mais ayant un impact combiné sur les acteurs. Autrement dit: "It reveals the skeletal structure of those social systems where decisions interact, and it reveals, therefore, the essential structure of both conflict and cooperation" (Rappoport 65:front cover). Toutefois, malgré ces postulats de généralité, la théorie des jeux (en tout cas au plan de son outillage mathématique) est essentiellement une théorie normative des choix (et nécessairement du calcul des résultats). Elle n'est opérationnelle que sous des nombreuses conditions ceteris paribus.

Les ingrédients d'un jeu

Il est important de discuter les points essentiels d'un modèle, car ils définissent les éléments d'un langage que le chercheur surimpose à la réalité . Dans la théorie des jeux, les éléments centraux du modèle sont (1) la définition d'un jeu et (2) les stratégies rationnelles qu'on peut attribuer aux joueurs.

Les ingrédients de base d'un jeu sont implicitement donnés par le nom "théorie des jeux": il y a des joueurs (acteurs), des rétributions (gains et pertes) et des règles du jeu. N'importe quelle unité poursuivant des buts d'une façon autonome peut être joueuse, donc il peut s'agir d'Etats, d'organisations ou encore de personnes. Les règles définissent les variables qu'un joueur peut contrôler: par exemple des possibilités de choix, d'information et de communication entre joueurs. Elles déterminent également les rétributions, les bénéfices négatifs (pertes) ou positifs qui résultent des choix de tous les joueurs. La notion de "game" est donc plutôt utilisée pour décrire les règles d'un jeu (au sens large du terme), tandis que la notion de "play" définit la "partie" (l'instance concrète d'un jeu).

Par rapport à nos recherches, l'aspect le plus intéressant de la théorie des jeux est celui de la stratégie, c'est-à-dire la procédure de décision que doivent prendre les joueurs pour optimiser leurs gains. Examinons ce concept à l'aide d'un exemple simple. Rappoport (66:18) définit la théorie des jeux par son objet, à savoir les situations ayant les caractéristiques suivantes:

  1. Il existe au moins deux joueurs.

  2. Le jeu débute par le choix effectué par un joueur parmi plusieurs alternatives.

  3. Ce premier choix définit une certaine situation qui détermine le choix suivant (qui et quoi).

  4. Les choix opérés par un joueur peuvent ou pas être connus par les autres joueurs.

  5. Si l'on décrit un jeu par ces choix successifs, il existe une règle pour la fin du jeu.

  6. La situation finale d'un jeu détermine la rétribution de chaque participant.

D'un point de vue procédural, un jeu est donc un ensemble de situations de décision à l'intérieur duquel les joueurs choisissent entre les actions possibles. Chaque choix (ou action) est connecté à un ensemble de résultats possibles décrits par valeur sur des échelles de préférence (qui peuvent être "ordinales", "par intervalle" ou "cardinales"). Dans la théorie des jeux, ces résultats sont en règle générale les mêmes pour tous les joueurs (angl. "interpersonnally exchangable"). Une chaîne de décision dans un jeu est donc un ensemble de choix déterminé par les utilités et les probabilités successives de résultats. Cette approche peut donner l'impression que les jeux sont déterministes, à condition que les joueurs agissent rationnellement. Toutefois, ceci est faux pour certains types de jeux; par exemple, il existe des jeux où le profit maximal n'est possible qu'à la suite d'une coopération entre joueurs.

La rationalité de base de la théorie des jeux est une règle de maximisation du profit individuel. Les joueurs doivent trouver une stratégie qui leur garantisse une utilité minimale dans toutes les circonstances. Dans des cas simples, il existe deux joueurs antagonistes qui ne communiquent pas, qui minimisent leur risque et qui supposent que l'opposant se comporte d'une façon rationnelle. A l'aide du jeu

dans la figure 3-1 "Exemple de jeu à somme nulle" [p. 58], nous allons brièvement expliquer ces concepts et nous allons introduire la règle du "minimax". Ce jeu est un jeu à deux personnes à somme nulle, c'est-à-dire ce que l'un perd, l'autre le gagne. Chaque joueur possède deux stratégies (A1,A2 et B1,B2) La matrice montre les quatre résultats possibles résultant du choix de ces stratégies. Le joueur "ligne" A choisit la stratégie (représentée par une ligne dans la matrice) qui lui permet de maximiser son gain minimal. Par conséquent, il choisit la deuxième ligne A2 où il assure un gain minimal de 1 (8 est plus élevé que -5 et 1 est plus élevé que -7 de la stratégie une). Le joueur B choisit également la stratégie B2 pour les mêmes raisons (en fait il le ferait même s'il pensait que A était irrationnel). Ce jeu possède un équilibre stable {A2, B2; (1/-1)} et il est déterministe. Dans ce type de jeu, A et B vont toujours choisir une stratégie qui contient un "saddle-point" s'ils sont rationnels.

Ce principe peut être généralisé pour toutes sortes de jeux où l'on connaît la matrice des gains et des pertes. En règle générale, le joueur d'un jeu antagoniste sans communication possible entre joueurs doit toujours maximiser son gain minimal, même dans les circonstances où le résultat n'est plus garanti. Souvent ces points d'équilibre n'ont qu'une définition statistique. Le raisonnement simple et déterministe ne fonctionne donc que pour une classe très réduite de jeux relativement simples. Certains types de jeux ne permettent pas de construire une matrice de jeu, car il n'existe plus de solution rationnelle (y compris celles de type statistique). Nous n'allons pas discuter les propriétés de jeux très complexes, par contre nous allons nous pencher sur le problème des jeux à rationalités multiples ou paradoxales tel qu'on le retrouve dans le "dilemme du prisonnier". Ce jeu relativise l'importance des règles de maximisation individuelle du profit chères à certaines théories de la décision rationnelle*1.

Jeux de conflit et de coopération

Les jeux de conflit et de coopération tiennent une place très importante dans la littérature en science politique. La science politique utilise souvent ces jeux-là pour décrire d'une façon formelle des situations de conflit et de coopération ou, comme le remarque Rappoport (66:214), pour mettre en évidence le "squelette" d'une situation. Les exemples les plus populaires ont montré que la maximisation du profit individuel à court terme peut conduire à des désastres à court ou à long terme.

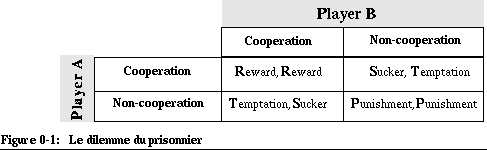
Le dilemme du prisonnier dont la matrice se trouve représentée dans la figure 3-2 "Le dilemme du prisonnier" [p. 59] est le plus connu de ces jeux. Il ne sert pas seulement d'exemple d'introduction à la théorie des jeux, mais également de cadre à des expériences psycho-sociologiques très intéressantes. Si A et B coopèrent dans ce jeu, les deux vont être récompensés ("reward", étant donné les circonstances). Si par contre A ne coopère pas et que B coopère, A va gagner gros ("temptation") et B va perdre gros ("sucker"). Si les deux ne coopèrent pas, les deux vont être punis ("punishment"). Si l'on suppose (comme on le fait en règle générale pour ces jeux simples) que A et B jouent une seule fois, qu'ils ne peuvent pas communiquer et qu'ils n'ont pas les moyens de s'assurer de leur coopération, le choix des joueurs doit se faire dans l'incertitude. Ils ne contrôlent pas toutes les variables de la décision.

Si l'on applique maintenant la stratégie "maximin"*2, c'est-à-dire le principe selon lequel chaque joueur doit maximiser son gain minimal (éviter d'être le "sucker"), on arrive à la punition. En effet, la stratégie "maximin" est "N" (non-coopération) pour les deux joueurs. On dit qu'elle est dominante parce qu'elle est choisie par le joueur rationnel. Nous deux joueurs arrivent donc à un résultat qui n'est pas optimal pour les deux. En situation (P,P) les deux sont dans une situation moins bonne qu'en (R,R) où les deux bénéficient de leur coopération mutuelle. Toutefois, alors que le résultat (P,P) est stable, ce n'est pas le cas pour (R,R) qui donne naissance au "dilemme du prisonnier". Une stratégie optimale selon la rationalité individuelle ne garantit donc pas forcément un bon résultat.

Il est intéressant d'observer comment des sujets expérimentaux se comportent dans ce jeu. Dans ce type d'expériences, on fait jouer le jeu à plusieurs reprises. A chaque tour, le joueur peut faire son choix en fonction des résultats des tours précédents. La stratégie simple qui donne le plus de succès au plan de la maximisation absolue (et non seulement relative) du profit est "tit-for-tat", c'est-à-dire la réciprocité conditionnelle. Elle se caractérise par le choix de la coopération la première fois, puis faire la même chose que l'autre aux coups précédents, un résultat obtenu suite à des analyses de tournois sur ordinateur Axelrod (1984). *3 Cette "rationalité" du "tit-for-tat" s'explique par le fait que chaque violation d'une coopération entraîne très vraisemblement une vengeance, et donc une baisse de profit à la longue. Les chances qu'une coopération s'établisse sont assez élevées dans ces expériences, surtout lorsque la fin du jeu est inconnue, c'est-à-dire si les joueurs ne savent pas quand le dernier round aura lieu. Parmi les sujets humains, la stratégie du "tit for tat" est assez populaire; souvent, elle est apprise après plusieurs tours; son choix dépend donc de la capacité d'apprentissage du sujet. Dans les jeux à tours fixés à l'avance, chaque joueur peut casser la coopération vers la fin afin de maximiser son ultime gain personnel. Chaque participant à un dilemme du prisonnier séquentiel doit posséder un ensemble d'heuristiques qui l'aident à prendre des décisions, mais qui ne peuvent pas garantir une stratégie optimale.

Un autre jeu très simple démontre également qu'il existe des situations où aucun choix rationnel individuel ne peut être conseillé. Rappoport (86:119) cite le jeu suivant: trois joueurs doivent partager 100 unités monétaires entre eux par une décision majoritaire (chacun votant au même instant). Ils ont le droit de communiquer entre eux et ils peuvent également s'isoler à deux pour discuter des alliances. Chaque joueur peut essayer de maximiser son propre profit en garantissant à un autre joueur un gain faible (ce qui est toujours mieux que rien). Les chances qu'une coopération s'établisse sont bonnes s'il existe un impératif (par exemple un contrat ou un rapport de force, etc.) de renforcer les gains collectifs. Une solution rationnelle simple à ce problème n'existe donc pas. La théorie ne peut que suggérer des solutions collectives qui se situent plutôt au niveau normatif des partages d'un bien. Cet exemple illustre que, plus une situation de "jeu" devient complexe, moins les enseignements de la théorie des jeux mathématiques deviennent instrumentaux pour expliquer ou conseiller un choix. Dans les termes de Rappoport (68:121) nous nous éloignons d'une théorie de la décision stratégique vers une théorie de la résolution des conflits. *4 La rationalité individuelle pure n'a de sens que dans des contextes très isolés. Un choix dans une situation complexe se réfère toujours à des structures collectives de signification et à des heuristiques qui permettent de les gérer.

Apprendre les stratégies

On peut également se demander comment les sujets apprennent à jouer un jeu. La théorie des jeux classique ne fournit que la recette pour la stratégie optimale (si elle existe) sans expliquer pourquoi les sujets l'utilisent ou non. Nous n'entrerons pas dans la question de savoir si la stratégie du "maximin" (ou de ses dérivés plus compliqués) est toujours optimale (elle néglige les avantages du coup dangereux à faible risque par exemple). Mais il faut constater que, pour la plupart des jeux imaginables, la stratégie à conseiller dépend plutôt du domaine social ou encore d'un savoir-faire difficilement réductible à une logique simple du calcul subjectif d'utilité du type "maximin". Pour trouver la stratégie optimale dans un dilemme de prisonnier à répétition, il a fallu avoir recours à des algorithmes génétiques inventés par Holland (cf. Axelrod 84). Ces algorithmes permettent à un système d'apprendre et surtout de sélectionner des règles de choix. Ils opèrent complètement en dehors de la théorie des jeux et fonctionnent grâce à un mécanisme de rétribution des règles qui conduit à des choix à succès dans le jeux. Ces algorithmes ont des propriétés intéressantes malgré leur "coût" computationel très élevé.

Vers la négociation des jeux

La théorie des jeux suppose en règle générale que les gains et les pertes d'un jeu sont fixés à l'avance. A la limite, les joueurs ont le "droit" de négocier leurs choix entre eux mais il n'est pas question de choisir le jeu à jouer ou encore la définition de la matrice des gains et des pertes. Dans le monde empirique, il existe beaucoup de situations où le joueur négocie le jeu qu'il va jouer. Imaginons un joueur qui est dans une situation de pertes ou encore de grande insécurité. Dans ces cas, il essaiera de négocier un compromis avec son adversaire, compromis qui, tout en étant avantageux pour l'adversaire, est toujours plus avantageux qu'une perte totale. A ce sujet, Rappoport (66:214) remarque que "game-theoretical analysis if pursued to its completion, perforce leads us to consider other than strategic modes of thought". Un de ces modes de pensée serait de jouer des jeux avec le but de définir des jeux. Dans Alker (80c), on trouve une analyse de la crise de Berlin qui va exactement dans ce sens. Les joueurs transforment un conflit qui a la forme du dilemme du prisonnier (avec une issue fatale pour les deux) en un jeu de "chicken"*5. On retrouve ici non seulement l'importance des représentations du monde (comme dans l'exemple précédent), mais également la capacité réflexive et communicative de l'acteur humain. Pouvoir négocier le jeu auquel on joue est tout aussi important que de savoir bien le jouer.

Les apports potentiels de la théorie des jeux pour l'analyse du décideur sont difficiles à évaluer. A partir de la discussion qui précède, on peut définir trois utilisations très différentes:

Le côté élégant et formel de la théorie des jeux est très séduisant au point que, par exemple, un auteur comme Ordeshook (92), écrit un livre intitulé "A Political Theory Primer" qui ne parle que de la théorie des jeux. Ce livre montre à la fois l'intérêt toujours vif de la science politique pour ce genre de modélisation*7 et aussi le fait que les prémisses de base sont restées les mêmes ces deux dernières décennies. Dans l'introduction de ce livre, l'auteur admet bien les limites du "rational choice". Mais il se réfugie derrière la notion de faire de la "first principle science" dont la tâche serait de mettre en évidence des vérités premières indépendantes de la réalité complexe du monde politique et des propriétés cognitives du décideur. Dans ce livre, l'auteur présente des modèles de jeux plus compliqués que les petits exemples qu'on vient de discuter. Il formalise par exemple l'absence partielle d'information dans des arbres de décision avec des modèles Bayesiens. L'idée que l'information n'est pas simplement absente ou présente, ou incomplète, mais peut-être contradictoire ne s'y retrouve presque pas. Pire, l'idée que le décideur politique n'est pas mathématicien est totalement ignorée. Même s'il l'était (par exemple grâce à des logiciels de support à la décision), la question du coût de calcul pour optenir un résultat optimal semble être négligée *8. Il n'est pas surprenant de constater toute absence de références empiriques dans ce livre - ceci en contraste avec la littérature sur l'intelligence artificielle dans les relations internationales. Quand l'auteur (Ordeshook 92:5) affirme que la rationalité ne peut être modélisée autrement que par ce type de modélisation mathématique, il a clairement tort.

Les ingrédients d'un jeu
Jeux de conflit et de coopération
Apprendre les stratégies
Vers la négociation des jeux
THESE présentée par Daniel Schneider - 19 OCT 94

Generated with WebMaker