En ingles
Dirk Danckaert
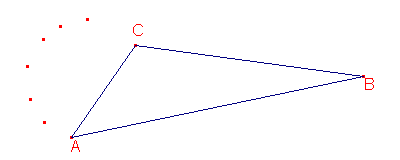
Despues de determinar algunos puntos aproximadamente, puede verse que la solución es un círculo que pasa por dos vértices del triángulo.

Así que construyo la mediatriz de ese lado, coloco un punto sobre ella y trazo el círculo que pasa por los dos vértices. Luego ajusto la posición del centro para que el triángulo simétrico-lateral sea rectángulo.
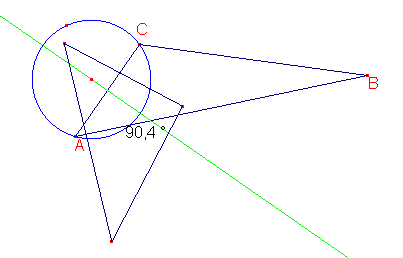
Al trazar los radios correspondientes a los vértices, parece ser que el ángulo formado con el lado del triángulo es igual al ángulo opuesto del triángulo de referencia.
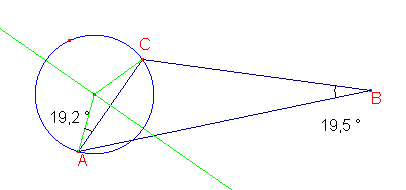
Entonces hago rotar la recta AC alrededor de A según el ángulo ABC, y determino la intersección de esta recta con la mediatriz de AC. Trazo el círculo con centro en esa intersección y que pasa por A. Todos los puntos de este círculo producen simétricos laterales rectángulos.
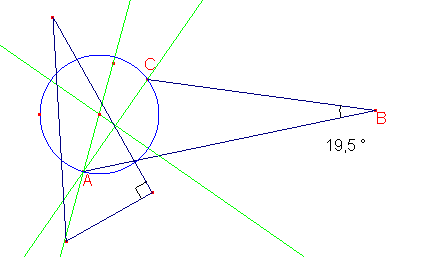
Primero construí un triangulo
rectángulo ADE y encontré que cuando el punto P estaba sobre
la recta que contenía la hipotenusa el triángulo simétrico
lateral de P era rectángulo
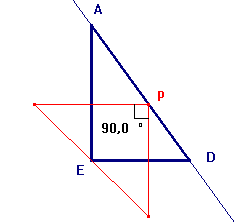
Así que pensé que debía
ocurrir lo mismo con los demás triángulos es decir el punto
P debía estar sobre una recta.
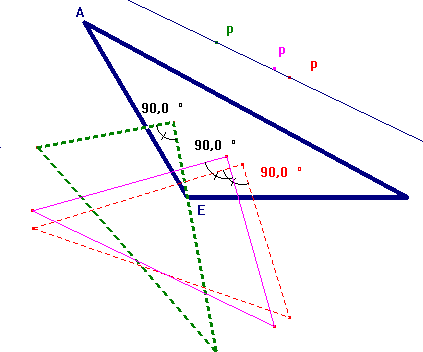
Luego decidí trabajar en compañía de pablo y el me dijo que alguno puntos estaban sobre el incentro es decir que estaban sobre una circunferencia lo que contradecía mi hipótesis
Decidimos construir un triangulo cualquiera y verificar las dos hipótesis
Los tres primeros puntos parecían estar alineados (en seguida pensamos que la hipótesis de la recta podría ser correcta)
Así que decidimos construir mas puntos para comprobarla
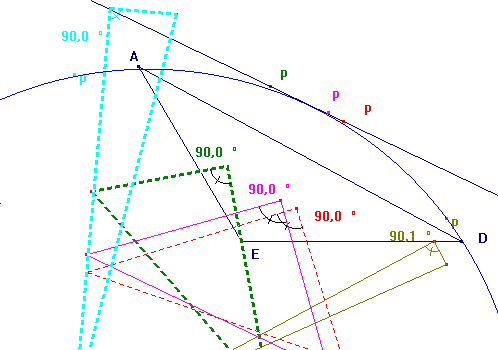
Para nuestra sorpresa la trayectoria
de los puntos no parecía ser una línea recta si no que parecían
formar una circunferencia aunque teníamos dificultad en ubicarlos
todos sobre la circunferencia
Así que decidimos comenzar
de nuevo construyendo el triangulo inicial ADE más pequeño
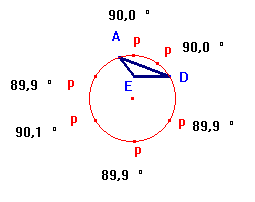
Construimos el triangulo ADE luego construimos los puntos P espaciados ocultamos los simétricos laterales y solo dejamos la medida del ángulo
Construimos una circunferencia arbitraria
y la acomodamos para que pasara por todos los puntos. Con esto quedamos
convencidos que la trayectoria era una circunferencia, el problema se reducía
ahora a encontrar un método para construirla
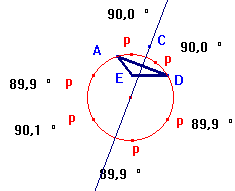
Primero construimos el circuncentro del triángulo ADE , al tratar de relacionar el circuncentro con el centro de la circunferencia buscada, encontramos que si trazábamos una perpendicular al lado AD que pasara por C esta recta también pasaba por el centro de la circunferencia.
Con esto ya teníamos que el
centro de la circunferencia estaba sobre la perpendicular, el problema
se reducía a encontrar en que parte de esa recta se ubicaba exactamente.
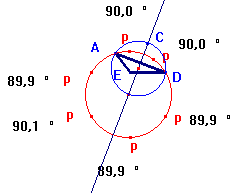
Luego construí el punto medio
del punto C y el centro de las circunferencia tratamos de relacionar este
punto medio con los puntos notables del triángulo ADE sin éxito.
Como la circunferencia buscada pasa por dos de los vértices del
triángulo ADE decidimos construir una circunferencia con centro
en el punto medio y radio en uno de los dos vértices y observamos
que también pasaba por el circuncentro C
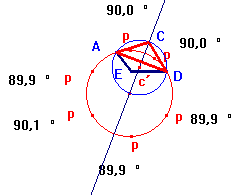
Sabemos que si una circunferencia
pasa por tres puntos entonces es el circuncentro del triangulo formado
por esos tres puntos. Así que decidimos construir el triangulo ADC
y hallarle el circuncentro C´
Es decir que el punto de intersección de la perpendicular y la circunferencia cuyo centro es el punto C´ Y cuyo radio es C, es el centro de la circunferencia buscada
Lo único queda por definir es por donde pasa el radio de la circunferencia buscada, pero como podemos observar el radio pasa por dos de los vértices del triángulo ADE
Creo que he resuelto el Problema del Triángulo Imagen Lateral Rectángulo
La solución completa del problema esta constituida por tres circunferencias cuyos centros se encuentran en los puntos K1, K2 y K3 constituidos por las Intersecciones de las Mediatrices de los lados, y Rectas que pasan por los vértices opuestos al lado en que se toman las mediatrices y el Punto de Lemoyne. Los radios son las distancias de los puntos K1, K2 y K3 a los vértices de los lados sobre los que se determinó las mediatrices.
UTILICE EL SIGUIENTE PROCESO
1 – Construí un triángulo cualquiera ABC y determiné un punto P.
2 – Obtuve las imágenes: A’ y B’ de P, respecto a los lados AB y AC y trace el segmento A’B’
3 – Constrí una recta perpendicular al segmento A’B’ en el extremo B’ .
4 – Obtuve la imagen C’, del punto P, respecto al lado BC.
Ahora bién, se obtienen soluciones cuando el punto C’ se encuentra sobre la recta A’B’. Así obtuve varios puntos de solución aproximada.
Comprobé que los puntos soluciones aproximadas no se encontraban alineados y pensé que tal vez se encontraban sobre un arco de circunferencia.
Para determinar la "posible circunferencia", tracé segmentos entre los puntos soluciones aproximadas consecutivos, determiné los puntos medios de esos segmentos y luego tracé mediatrices. Las mediatrices parecían concurrir en un punto.
Los siguientes pasos fueron en sentido contrario:
1 - Construí el triángulo ABC, determiné la Mediatríz del lado AB y coloque un punto K, sobre ella.
2 – Construí una circunferencia con centro en K, un Radio Cualquiera y coloqué un punto P sobre ella.
3 – Determiné el Triángulo Imagen lateral de P y luego manipulé tanto el punto K, como el Radio de la circunferencia, para tratar de obtener Triángulos Imágenes Laterales Rectángulos.
4 – Descubrí que cuando las circunferencias centradas en K tiene por radio el segmento KB (que es el mismo AK) el ángulo A’ del Triángulo Imagen Lateral permanece constante. ¡EUREKA! Ahora Solo faltaba determinar, exactamente, en que lugar de la Mediatríz debería estar el punto K.
5 – Realicé varias pruebas hasta que encontré que debería estar en la intersección de la Mediatríz con la recta Vértice Opuesto Lemoyne.
Construyo el triángulo, escojo
uno de los ángulos, lo mido y desplazo el punto libre M hasta que
sea de 90°.
Coloco un punto en esa posición
;
repito este procedimiento para nuevas
posiciones de M y constato que el lugar parece un círculo que pasa
por dos vértices del triángulo de referencia.
Concluyo que el lugar estará formado de tres círculos que pasan por dos vértices del triángulo de referencia.
Coloco puntos móviles sobre las tres mediatrices del triángulo de referencia, construyo los círculos que pasan por uno de ellos y dos vértices del triángulo; muevo los puntos móviles para que el triángulo simétrico-lateral sea rectangulo (control por medida); la codificación con colores me permite ubicarme mejor.
Al construir el triángulo formado por los centros de los tres circulos, aparentemente los lados pasan por los vértices del triángulo de referencia.
etapa infructuosa
Trazo los circulos que pasan por
M y dos vértices del triángulo de referencia.
Nada particular, pero construi el
circuncírculo del triángulo de referencia que me dará
la solución...
Retomo la idea de Sol2, encuentro un método para deducri dos lugares a partir del primero y al trazar los lados del triángulo gris que pasan por los centros de los tres círculos, constato que son tangentes al circuncírculo: esa es mi solución
solución :
circuncírculo del triángulo
de referencia
Tangentes al circuncirculo por los
vértices del triángulo
Esas tangentes se cortan dos a dos
en los centros de los círculos solucion.
Esos círculos pasan por los
vértices del triángulo de referencia.
Complete el rectángulo doble
del triángulo solución y constaté que el lugar del
cuarto vértice es un círculo concéntrico al círculo
solución correspondiente...