1. Demostración de un caso particular:

Queda la pregunta de por qué para todo P tal que APC=90-ABC, PaPbPc es rectangulo.

Explorando la construcción comencé a mover P, y descubrí un caso especial en el que la construcción se simplifica: cuando P está sobre la recta BC. En este caso P=Pa. Construi los segmentos AP, APb y APc, que son congruentes y forman triangulos isosceles. En esta configuracion, P,A y Pc estan alineados.



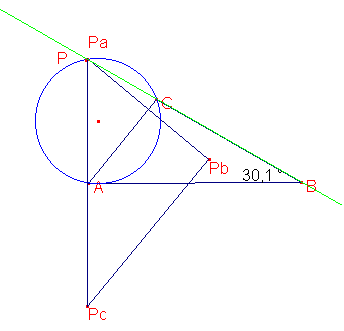
Como PPc es perpendicular a AB, se forman dos triangulos semejantes: PAM (donde M es la proyeccion ortogonal de P sobre AC) y PPcPb. Como son simetricos, PPc=2PA y PPb=2PM, por lo tanto son semejantes. Como PMA es rectangulo, entonces PPbPc tambien lo es.

2. Demostracion general:

Al explorar el caso general de APC=90-ABC, descubrí que había otras congruencias de angulos. En particular, PcPPb=CAB, APbPa=CAB y PcAPb=2CAB.

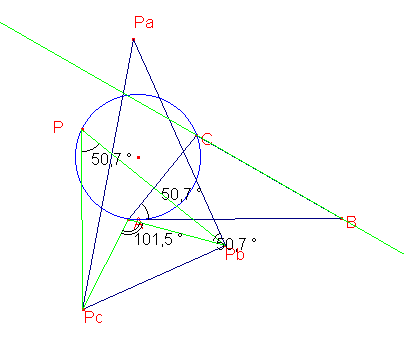
Como el triángulo PcAPb es isosceles, las dos ultimas igualdades constituyen una explicacion de que PcPbPa sea rectangulo, pues implican que PbPa sea paralelo a la bisectriz de PcAPb.

Faltaba entonces demostrar esas igualdades.

Al redefinir P como punto libre, descubrí que se conservaba PcPPb=CAB y PcAPb=2CAB, pero se perdía APbPa=CAB.

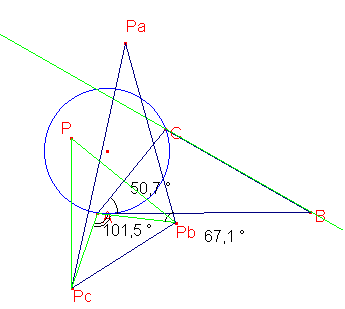
Así que las primeras dos igualdades se debían a la simetría, la otra al hecho de que APC=90-ABC. Decídí entonces tomar solo las rectas AB y AC y el punto P. Al construir los simetricos de AP con respecto a las dos rectas, caí en la cuenta de que había una composicion de simetrías axiales. AP es simetrico de APb y APc es simetrico de AP. Como toda composicion de simetrias de ejes secantes es una rotacion del doble del angulo entre los ejes, quedaba demostrado que PcAPb=2CAB.

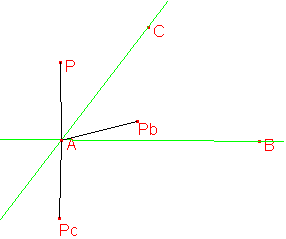
Luego descubrí otra propiedad invariante: APC-APbPa es constante. Al observar de nuevo la configuracion, descubrí que ese angulo es PaPbC.

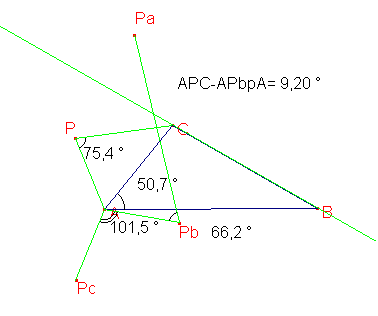
Al mirar la simetría de P con respecto a BC, pude verificar que PbCPa=2PCA+2PC(-B), es decir que

PbCPa=2(180-BCA). Como PbPaC es un triángulo isosceles, puede calcularse PaPbC

PaPbC=(180-PbCPa)/2

= (180-2(180-BCA))/2

=(180-360+2BCA)/2

=(2BCA-180)/2

=BCA-90

Luego

APC-APbPa=PaPbC=BCA-90

Si APbPa = BAC, entonces

APC=BCA-90+BAC

APC= BCA+BAC-90

APC=180-ABC-90

APC=90-ABC.