The input of the simulation is the experiment that the learner has built in the LAB. In an experiment, pseudo-subjects are supposed to memorize words or other items and later try to remember them. The output of the simulation is the list of words that each subject has remembered. The constraints that justify our design choices are related to the pedagogical function of MM and to the nature of available knowledge.
Minimal Validity Rule: if the learner builds an experimental plan with a factor F and based on a paradigm P, and if the literature includes knowledge on the effects of factor F, within the paradigm P, then the simulation must produce data in which the effects F can be identified. More than being precise, the results must be explainable. Several ILE designers (White and Frederiksen, 1988; Roschelle, 1988) have shown that a qualitative simulation, although less efficient, is better suited to pedagogical purposes. Simulating an experiment involves an analysis of the structure and content of this experiment. The simulation produces a trace that can be used in explanation. It consists of pre-stored comments and keywords. We are exploring the possibility for MM to generate a trace structured in hypertext form. This would allow the learner to read the explanation at the level of detail that he wants.
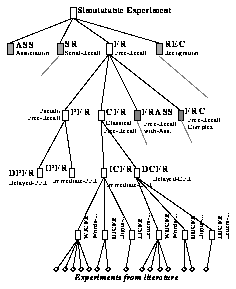
Moreover, the literature does not cover the very large space of experiments that can be designed in MEMOLAB. Within the space of possible experiments, psychologists have concentrated their work on some avenues, or paradigms. (In experimental psychology, a paradigm is defined as a class of experiments.)The comparison of experiments within a paradigm brings more information than comparing experiments which differ in too many ways. Therefore, the case-retrieval process is not a simple search through a flat set of cases, with some similarity metrics. The set of cases (literature experiments) is partitioned into paradigms and a main stage during the simulation consists in identifying the relevant paradigm (see below, the paradigmatic analysis).
Another peculiarity of this domain is that the adaptation of the retrieved case to the target case cannot be driven by universal rules. Let us imagine that the learner builds an experiment where subjects have to memorize a long list of words and that MM retrieves an experiment which is similar on all points but the list length. The effect of list length is not universal, but varies according to other factors such as the delay between the memorizing and recall events. Therefore, case-adaptation is performed by a set of rules (named Vertical Adapters) that differ for each paradigm. In short, case-adaptation in MM is governed by rules that are themselves case-dependent.
Figure 10: The paradigm discrimination tree or structure of cases in the simulation
The structure analysis returns the factors identified within the learner's plan and the value (modality) of this factor in each sequence. This knowledge feeds the paradigmatic analysis process which identifies the most specific paradigm (leaf node) corresponding to the learner's sequence. (The word `paradigmatic' refers here to the meaning used in experimental psychology, as specified above.)
Let us consider first the simplest simulation process, i. e. computing the results for a sequence si. This sequence si is matched against the discrimination rule of each node N of the paradigm tree. If the match is positive, we store the vertical adapters of N and recurse on descending nodes. When a leaf node is reached, the associated set of literature sequences S'i = {s'i. 1, s'i. 2, ... , s'i. n } is retrieved. In addition, vertical adaptation rules have been collected through the tree: VAi = {vai. 1, vai. 2,. . . , vai. m }. The selection process reasons on VAi in order to select among S'i the experimental sequence s'i which is the most similar to si. The last stage is to retrieve the data of s'i - denoted D'i - stored with s'i, and to execute VA in order to compute Di:
Let us imagine that the learner's experiment includes two sequences s1 and s2. We can apply independently the same algorithm on each sequence and generate results for each sequence:
However, this independent processing does not respect the minimal validity rule expressed above. Let us assume that between s1 and s2, the learner has created some systematic differences in order to observe the effect e of factor f (denoted ef). With independent sequence processing, we cannot guarantee that, when learners will compare D1 and D2, they will find ef. In order to guarantee that differences between D1 and D2 correspond to the expected effect, one must generate D2 from D1 and what we know about ef. When s1 and s2 are compared to a tree node, the effects stored with that node are compared to the structure of (s1,s2). This structure was determined during the structure analysis stage. If ef is identified, the Horizontal Adapters (HAs) that are associated with ef are stored. Then, the experiment is `reduced', i. e. only s1 is passed to lower nodes. Data for s2 will be generated from D1 and the VA of ef.
These two strategies are summarized in Figure 11. The optimal strategy is applied when a known effect is identified within the learner's experiment and if this effect does not interact with other factors. The optimal solution can be applied on parts of the learner's experiments.
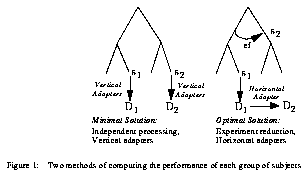 Figure 11: Two methods of computing the performance of each group of subjects
Figure 11: Two methods of computing the performance of each group of subjects
 Figure 12: Three of the four panes of the window presenting the output of the simulation. (The graphics pane can be shifted with the `row data' pane). The bold names in the simulation trace are external hypertext buttons.
Figure 12: Three of the four panes of the window presenting the output of the simulation. (The graphics pane can be shifted with the `row data' pane). The bold names in the simulation trace are external hypertext buttons.
In the current version of Memolab, the simulation tool includes the data tools and statistical tools that we first designed as independent tools. We integrated them into the simulation to simplify the environment (which had then too many windows). Our original project intended to have some tutoring related to the analysis of experimental output, both for the statistical processing and for interpreting results with respect to hypotheses. MEMOLAB would then have covered the whole reasoning cycle of an experimental psychologist. However, the focus placed on ETOILE led us to reduce the amount of energy invested in MEMOLAB and to concentrate on the methodology of experimentation.