6-2.3 Simulation numérique et règles d'inférence

Les systèmes à bases de règles peuvent avoir plusieurs fonctions en rapport avec la simulation numérique. Nous nous intéressons ici plus particulièrement à la modélisation des décideurs qui interviendront au plan technique surtout pour modifier des flux ou des paramètres. Une autre fonction qu'on ne discutera pas ici serait par exemple l'assistance à la modélisation (utilisation du logiciel, interprétation des résultats etc). Au plan technique, nous nous intéressons ici à l'emploi de règles dans un modèle et à leur interaction avec les valeurs ou les équations de la simulation. Avant de montrer et de discuter un tel mécanisme, nous allons brièvement décrire un moteur d'inférence que nous avions réalisé dans le cadre d'un projet que nous avons appelé AIPSS[83].

L'inférence par un moteur de chaînage avant

Nous avons écrit une interface entre un moteur de chaînage avant et ce langage de simulation discrète. Le principe d'un tel langage repose sur les "production systems". Rappelons qu'un "système de production" contient les éléments suivants[84]:

1. Un jeu de règles (de production)
2. Une base de données avec des faits
3. Un interpréteur qui utilise (1) et (2) afin de "calculer".

Dans un système de production à chaînage avant simple, une règle possède la forme suivante:

    Si <SITUATION> alors <ACTION> 

Ceci signifie que si l'interpréteur trouve dans la base de données un fait (aussi appelé situation ou condition) qui correspond à la "situation" (aussi appelée "côté gauche" ou conditionnel de la règle), la règle est activée et son action (aussi appelée côté droit) est exécutée à un moment donné. Ainsi la fonction la plus importante de cet interpréteur (ou moteur d'inférence) est évaluative. Il travaille (un peu comme une montre de simulation) en cycles et regarde quelles règles il peut utiliser par rapport aux données qui se trouvent dans la base de données. Ensuite, sa deuxième fonction est éventuellement de choisir entre ces règles et de les exécuter. Dans le cas le plus "classique", l'exécution d'une action signifie l'écriture d'un autre fait dans la base de données. au plan logique, cette utilisation des règles peut être décrite avec les termes de "si-alors" ou de "condition-action". Toutefois, dans notre système, nous autorisons tout type d'action avec les règles (et même sur les règles), comme par exemple celle de manipuler des équations dans un modèle de simulation. La syntaxe d'une règle dans notre système est définie dans la figure 6-2.

Chaque règle doit posséder un nom et faire partie d'un système de règles. Ensuite, il est possible d'avoir plusieurs clauses "situation". Ces clauses "si" sont des chablons (angl. "patterns") qui doivent tous correspondre ("match") à un fait dans la base de données. Les variables doivent être unifiées, cela veut dire que les variables du même nom dans les différentes clauses de la situation doivent correspondre à des expressions dans les faits de la base de données. Tous les symboles précédés par un "-" sont des variables (comme les "?" dans le système de simulation discrète et les "!" dans Ross). Examinons l'exemple de la règle qui se trouve dans la même figure. Le côté "situation" possède deux clauses conditionnelles. Elles suivent le mot clé "lhs" (qui signifie "left hand side"). Cette règle est donc activée par exemple lorsque la base de données contient les faits:

		(food-reserves 100000) 
		(population 5000) 

Une règle n'est pas nécessairement exécutée dans tous les cas de correspondance (angl. "matching") réussie. Il existe en effet une clause "test". Cette clause doit être une expression "Scheme"[85] ordinaire et doit être vraie, (c'est-à-dire retourner la valeur de "vrai") pour que le côté droit - ce qui suit le mot clé "rhs" (right hand side) - soit exécutable. Dans le cas de nos deux faits ci-dessus, le test va échouer car il n'y pas moins de rations hebdomadaires de nourriture que de population (10000 est plus grand que 5000). Dans le cas contraire, la règle aurait pu être exécutée (à moins qu'un mécanisme de contrôle ne s'y soit opposé) et elle aurait écrit le fait "(goal find-food)" dans la base de données. Ce fait nouveau à son tour aurait déclenché d'autres règles. En ce qui concerne le côté droit de la règle (c'est-à-dire l'action), il s'agit d'une procédure "Scheme". Elle peut accéder à toutes les variables du côté gauche, ainsi qu'à des variables qui contiennent les faits liés dans la base de données. La variable =f1 correspond au fait "lié" à la première clause "si", =f2 au fait lié à la deuxième, etc. Ce mécanisme nous donne de nouveau une très grande flexibilité. On peut imaginer par exemple une clause:

(add-fact* '(goal find-food 
                ,(- -number-of-people rations-de-nourriture-hebdomadaires)) 
    afgh) 

qui insérera dans la base de données le fait "

		(goal find-food <ce qui manque>)

Notons ici que la procédure "add-fact" n'évalue pas son argument (les symboles sont rentrés "tel quels" dans la base de faits) tandis que "add-fact*" fait une telle évaluation. "Add-fact*" n'écrit donc pas simplement une expression dans une base de données, mais le résultat d'un calcul arbitraire. En conséquence il faut utiliser les conventions Scheme pour "quoter" (prendre les symboles "tel quel") la liste et "déquoter" (rendre "évaluable") l'expression arithmétique à évaluer. Nous n'allons pas discuter la puissance de ce mécanisme de computation, mais il convient de mentionner qu'il s'agit ici d'un mécanisme universel qui est plus particulièrement adapté à la formalisation d'un certain type de pensée quasi-rationnelle. Le principe est très simple, par contre son utilisation demande une certaine expérience en "knowledge engineering".

Simulation discrète et inférence

Comme le montre l'exemple décrit dans l'appendice A-2 "L'exemple «Demopolis»" [p. 379], il est faisable et intéressant de combiner les techniques de la simulation discrète et des systèmes d'inférence. On peut représenter des décideurs comme systèmes à base de règles (voir ci-dessus "L'inférence par un moteur de chaînage avant" [p. 246]).

Dans le petit langage que nous avons développé, on définit d'abord le système global (capable à la fois de simulation numérique et d'inférences).

(def-sib demopolis) 

Voici les quelques règles du système de simulation numérique qui modélisent l'évolution de la démographie d'un pays.

  (def-level ?pop sbs (demopolis) 
             ini (20000) 
             eq (+ ?pop ?Birth (- ?Death))) 
  (def-flow ?Birth sbs (demopolis) 
            ini (0) 
            eq (* ?Birthrate ?pop)) 
  (def-flow ?Death sbs (demopolis) 
            ini (0) 
            eq (* ?Deathrate ?pop)) 
  (def-parm ?Birthrate sbs (demopolis) ini (0.051)) 
  (def-parm ?Deathrate sbs (demopolis) ini (0.039)) 
  (def-obs ?occupation sbs (demopolis) 
           ini (0) 
           eq (/ ?pop 20000)) 

Ensuite on peut rajouter des systèmes d'inférence avec l' expression (def-ib....) et les définir comme des sous-systèmes du système global avec l'expression (sub-sys ...)..

;; The system which models the "people" 
(def-ib people) 
;; The system which models the "government" 
(def-ib government) 

(sub-sys demopolis demopolis) 
(sub-sys demopolis government) 
(sub-sys demopolis people) 

Pendant l'exécution du modèle, on insère les valeurs appropriées de la simulation après chaque cycle de simulation dans les bases de faits des "décideurs". On insère ces valeurs avec la syntaxe suivante: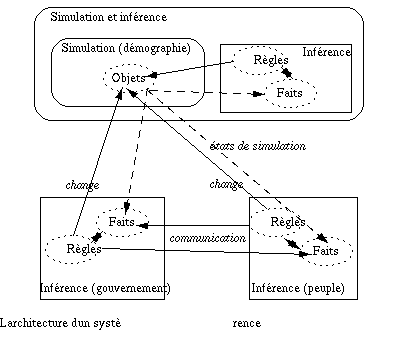

		(sys-var <?name> <simulation-object>)

Ces chablons seront dans la suite utilisés dans les conditionels des règles. La variable "?name" pointera sur l'objet de simulation (voir section 6-2.1 "La simulation numérique discrète" [p. 243]) et la règle peut y accéder et y effectuer des modifications comme c'est décrit plus bas. Les règles déclenchées ne peuvent donc pas seulement déclencher d'autres règles mais également modifier l'état de certaines variables de simulation, voire même les équations. La Figure 6-3: "L'architecture d'un système de simulation et d'inférence" [p. 250] donne un résumé des différentes interactions entre les composantes d'un tel système.

Ci-dessous on discutera une seule règle du petit système de démonstration (voir page 379). Cette règle (attribuée au "gouvernement") déclenche la mise en oeuvre d'allocations familiales lorsque l'occupation du territoire est trop basse.

p augment-births 
     ibs (government) 
     lhs (sim-cycle -t) 
         (family-allocation -x) 
         (sys-var ?occupation -occobj) 
     test (< (so-val -occobj) 0.945) 
          (not-fact (program birth-stimulation -n) government) 
     rhs (add-f* '(family allocation ,(+ -x 300) (time ,-t))) 
         (add-fact* '(family-allocation ,(+ -x 300) (time ,-t)) people) 
         (add-f* '(program birth-simulation ,(+ -t 12))) 
         (rm =f2) 
     ) 

Cette règle s'active avec les "patterns" suivants:

		lhs	(sim-cycle -t) 
        			(family-allocation -x) 
        			(sys-var ?occupation -occobj)

mais elle s'exécute uniquement lorsque le taux d'occupation du territoire est sous un certain seuil et si aucun programme de stimulation de naissances n'est déjà opérationnel:

		test 	(< (so-val -occobj) 0.945) 
			(not-fact (program birth-stimulation -n) government) 

La fonction "(so-val <simulation-object>)" retourne l'état d'un objet de simulation et la fonction "(so-def <simulation-object> <val>)" change l'état d'un objet. A noter aussi la différence entre les fonctions "add-f" et "add-fact". La première rajoute un fait à la propre base de données tandis que la deuxième sera utilisée pour rajouter un fait dans celle d'un autre "décideur".

		rhs 	(add-f* '(family allocation ,(+ -x 300) (time ,-t))) 
         			(add-fact* '(family-allocation ,(+ -x 300) (time ,-t)) people) 
			(add-f* '(program birth-simulation ,(+ -t 12))) 

Dans la trace d'exécution du modèle (voir A-2 "L'exemple «Demopolis»" [p. 379]) on peut voir l'effet de telles règles sur l'évolution d'un système dynamique. Il est clair que le modèle "demopolis" ne représente qu'un "proof of concept" technique[86], mais il montre le potentiel de cette combinaison de deux techniques.

La simulation numérique ordinaire fonctionne avec un principe de "ceteris paribus" qui ne tient pas compte des ajustements discrets par les systèmes de décisions qui peuvent intervenir dans le processus. On peut effectivement argumenter que la politique publique n'existe pas dans beaucoup de domaines (comme le système écologique mondial). Mais l'Histoire a bien montré qu'en cas de crise perçue, le système politique intervient. Donc, une simulation numérique ordinaire ne peut que modéliser ce qui va se passer sans intervention. Avec un tel système, on peut modéliser ce qui va se passer après des interventions. Cette étude conceptuelle a montré qu'il est très facile[87] d'interfacer un modèle de décision à un modèle d'environnement. La difficulté réside évidemment dans toute modélisation des décideurs.

La simulation numérique se prête bien à la modélisation d'un environnement quantifiable. Pour modéliser un système d'interactions entre objets qui ne peut pas être exprimé en termes de covariance, il faut utiliser une autre méthodologie: la simulation orientée objet que nous allons discuter dans la section suivante.