chapitre 6 Le décideur, son organisation et son environnement
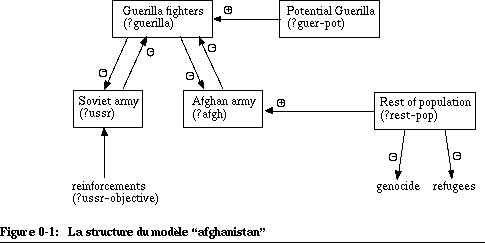
Dans notre langage de simulation numérique discrète d'événements, les niveaux doivent être bien différenciés des flux à cause de l'algorithme de calcul. Le modèle ci-dessus présente ce type de structure. Par contre, la manière de définir les objets de simulation (en termes traditionnels: les équations et les paramètres) reste très souple. C'est le modéliseur qui décide s'il préfère un modèle très compact ou très désagrégé avec beaucoup de variables. Ici, nous avons choisi de travailler avec relativement beaucoup d'objets par rapport au modèle d'origine. L'idée derrière ce choix est qu'il sera plus simple de les manipuler avec d'autres mécanismes, par exemple des systèmes d'inférence ou des simulations orientée objets. Voici les "équations" qui définissent le modèle:
; --- guerilla
(def-level ?guerilla sbs (*gen*) ini (155000)
eq (+ ?guerilla ?guer-gains (- ?guer-losses)))
(def-flow ?guer-gains sbs (*gen*) ini (0)
eq (* ?guer-gain-r ?guer-pot))
(def-parm ?guer-gain-r sbs (*gen*) ini (0.01))
(def-flow ?guer-losses sbs (*gen*) ini (0)
eq (* ?guer-loss-r ?guerilla (+ ?ussr ?afgh)))
(def-parm ?guer-loss-r sbs (*gen*) ini (0.00000035))
; -- potential guerilla
(def-level ?guer-pot sbs (*gen*) ini (1470000)
eq (- ?guer-pot ?guer-gains))
; -- rest of population
(def-level ?rest-pop sbs (*gen*) ini (10850000)
eq (- ?rest-pop ?army-recruits ?genocide ?refugees))
(def-parm ?army-recruits sbs (*gen*) ini (1500))
(def-flow ?genocide sbs (*gen*) ini (0)
eq (* 0.0011 ?rest-pop))
(def-flow ?refugees sbs (*gen*) ini (0)
eq (+ 120803))
; -- ussr army
(def-level ?ussr sbs (*gen*) ini (0)
eq (+ ?ussr ?ussr-flow (- ?ussr-losses)))
(def-flow ?ussr-flow sbs (*gen*) ini (0)
eq (- ?ussr-objective ?ussr))
(def-parm ?ussr-objective sbs (*gen*) ini (85000))
(def-flow ?ussr-losses sbs (*gen*) ini (0)
eq (* 0.003 ?guerilla))
; -- afghanistan
(def-level ?afgh sbs (*gen*) ini (35000)
eq (+ ?afgh ?army-recruits (- ?afgh-losses)))
(def-flow ?afgh-losses sbs (*gen*) ini (0)
eq (* 0.006 ?guerilla))
; -- observations
(def-obs ?guer-tot-losses sbs (*gen*) ini (0)
eq (+ ?guer-tot-losses ?guer-losses))
(def-obs ?ussr-tot-losses sbs (*gen*) ini (0)
eq (+ ?ussr-tot-losses ?ussr-losses))
(def-obs ?afgh-tot-losses sbs (*gen*) ini (0)
eq (+ ?afgh-tot-losses ?afgh-losses))
Voici les résultats d'une simulation:
==> (sim-plot *gen* 72) a = ?GUERILLA min: 167801.25 max: 252302.585649685 b = ?GUER-POT min: 712937.31430302 max: 1455300. c = ?REST-POP min: 1552781.45434478 max: 1.0715762e7 d = ?USSR min: 84243.092243051 max: 84535. e = ?AFGH min: 35570. max: 43998.9650902446 f = ?GUER-GAINS min: 7201.38701316182 max: 14700. g = ?GUER-LOSSES min: 1898.75 max: 10938.1432205581 h = ?GENOCIDE min: 1844.62198396161 max: 11935. i = ?REFUGEES min: 120803 max: 120803 j = ?USSR-FLOW min: 465. max: 85000 k = ?USSR-LOSSES min: 465. max: 756.907756949056 l = ?AFGH-LOSSES min: 930. max: 1513.81551389811 m = ?GUER-TOT-LOSSES min: 1898.75 max: 712241.155119586 n = ?USSR-TOT-LOSSES min: 465. max: 49500.5174548777 o = ?AFGH-TOT-LOSSES min: 930. max: 99001.0349097554 STEP 1: ** ea * g d * STEP 2: ** e a* g d ** STEP 3: * * e a * g d ** STEP 4: * * e a* dg ** STEP 5: * * e a * d g ** STEP 6: * * e * d g * * STEP 7: * * e da* g * * STEP 8: * * e d a* g * * [ ................ ] STEP 66: * ** d a * ge * STEP 67: * ** da * g e * STEP 68: *** ad * g e * STEP 69: ** a d * g e * STEP 70: ** a * g e* STEP 71: * a * d g *Le résultat de ce modèle était que la guérilla survivra (lettre a ci-dessus). Cela a été confirmé par l'histoire. Voici quelques valeurs de deux variables importantes d'observation, les pertes totales de la guérilla et des soviétiques.
==> (list-sim *gen* ?guer-tot-losses ?ussr-tot-losses)
SIM-I> LIST OF SIMULATION BASE *GEN* OBJECTS
?GUER-TOT-*?USSR-TOT-*
MAX : 712241.155 49500.517
MIN : 1898.750 465.000
STEP 0: 1898.750 465.000
STEP 1: 8952.569 968.404
STEP 2: 16349.533 1494.305
STEP 3: 24069.475 2041.238
STEP 4: 32091.955 2607.801
STEP 5: 40397.181 3192.659
.........
STEP 61: 619066.486 43208.591
STEP 62: 628657.773 43861.449
STEP 63: 638188.840 44509.182
STEP 64: 647659.400 45151.735
STEP 65: 657069.196 45789.055
STEP 66: 666418.003 46421.093
STEP 67: 675705.623 47047.802
STEP 68: 684931.887 47669.138
STEP 69: 694096.644 48285.061
STEP 70: 703199.769 48895.533
STEP 71: 712241.155 49500.517
Comparons ces résultats avec les résultats obtenus dans la simulation continue originale de Allan et Stahel. Avec leur méthode de calcul, ils arrivent après 72 cycles à 712'000 pertes pour la guérilla et à 49'000 pertes pour les Soviétiques. Notre modèle arrive à ces chiffres un cycle plus tôt, ce qui est un résultat excellent. En résumé, on peut donc formuler l'hypothèse que notre système calcule avec suffisamment de précision les résultats que l'on pourrait obtenir avec un langage de simulation utilisant des méthodes de calcul plus sophistiqués. Ces langages de simulation offre plusieurs avantages par rapport au notre, notamment la possibilité d'estimation de paramètres ce qui est crucial en simulation numérique de systèmes dynamiques. Cependant, une fois qu'un tel modèle a été créé, on peut le transporter sans grand danger dans notre système qui possède une flexibilité de modélisation très intéressante par rapport aux modèles mathématiques fermés. L'élément "discret" (c'est à dire les décisions) est primordial dans tout système social et une simulation mathématique ne peut pas le modéliser de la même façon*1.


Generated with WebMaker