Le triangle initial est appelé rvb (rouge, vert, bleu).
L’étude du triangle obtenu en prenant les symétriques d’un point quelconque M par rapport aux côtés rv, vb, br peut être ramenée à celle du triangle qui lui correspond dans une homothétie de centre M et de rapport ½ : il s’agit en définitive du triangle construit à partir des pieds Hb, Hr et Hv des perpendiculaires menées de M aux trois droites supports de rv, vb et br.
Méthode utilisée :
Le lieu de M quand l’aire du triangle HbHrHv est constante est un cercle dont le centre coïncide avec le centre du cercle circonscrit au triangle rvb.
À la différence du premier problème posé (triangle rectangle), il est assez difficile, par tâtonnement de rechercher différentes positions de M qui donnent une aire constante pour le triangle HrHvHb.
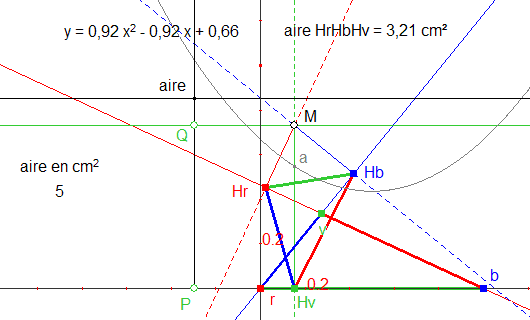
J’ai donc procédé de la sorte (voir figure 1) :

Figure 1
1. Je choisis un nombre (5) qui représente l’aire en centimètre carré du triangle (valeur modifiable, placée à gauche de la figure).
2. Je définis un repère orthonormé d’origine r et d’axe des x rb.
3. Je place un point quelconque P sur l’axe des abscisses, trace la perpendiculaire à l’axe des x en ce point et construit sur cette dernière une demi-droite d’origine P dirigée vers le haut.
4. Je reporte l’aire (5) sur cette demi-droite (point dénommé " aire ") et trace la parallèle en ce point à l’axe des x.
5. Je définis un point courant Q sur la droite Paire, trace la parallèle à l’axe des x en ce point et place un point courant M sur cette parallèle. J’ai donc défini le point M que je vais pouvoir déplacer en x et y.
6. Je mesure l’aire du triangle HrHvHb et reporte cette aire sur une demi-droite dirigée vers le haut, dont l’origine est sur l’axe des x et qui passe par M (point a).
7. Je crée le lieu de a par rapport à M et j’obtiens une parabole (en gris sur la figure).
Cette parabole d’équation y = ax^2 + bx + c est telle que c seul varie, quand l’ordonnée de M varie…
8. L’intersection de la parabole avec la droite d’ordonnée " aire " me permet de positionner M de façon à ce que l’aire de HrHbHv soit égale à la valeur de départ choisie (ici 5, voir figure 2).
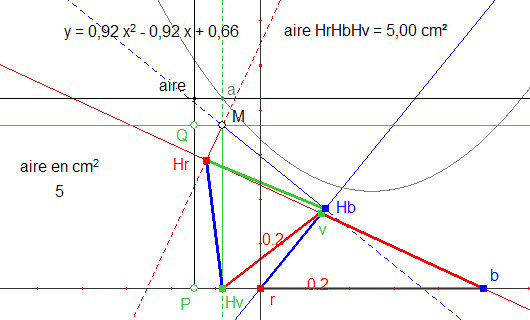
Figure 2
9. En modifiant l’ordonnée de M, je peux ensuite rechercher le lieu de M, point par point. Et je trouve le cercle annoncé au début.
10. Le fichier aireconstante2.fig (Cabri géomètre II Plus)
donne une animation.
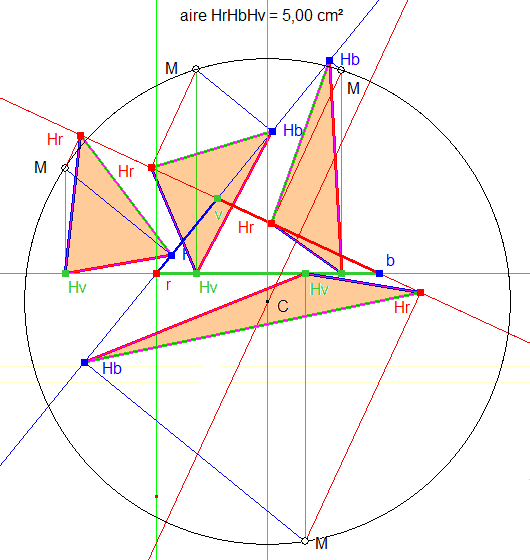
Figure 3
Voilà la formule de l'aire A' du triangle symétrico-latéral
quand le point décrit un cercle dont le centre est celui du cercle
circonscrit au triangle de base (lieu où l'aire est constante) :
A' = A*abs(1-(r/R)^2)
r : rayon du cercle portant le point M
R : rayon du cercle circonscrit
A : aire du triangle de base
J'ai trouvé ce résultat en traçant sur Excel
les courbes A' = f(r), puis A' = g(r^2) et en constatant que la seconde
était la réunion de deux droites.