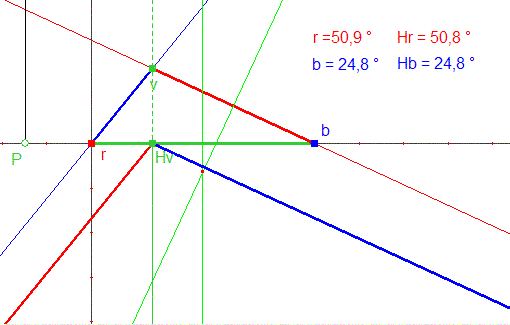
Le triangle initial est appelé rvb (rouge, vert, bleu).
L’étude du triangle obtenu en prenant les symétriques d’un point quelconque M par rapport aux côtés rv, vb, br peut être ramenée à celle du triangle qui lui correspond dans une homothétie de centre M et de rapport ½ : il s’agit en définitive du triangle construit à partir des pieds Hb, Hr et Hv des perpendiculaires menées de M aux trois droites supports de rv, vb et br.
Méthode utilisée pour trouver le lieu de M qui donne un triangle symétrico-latéral semblable
Je mesure deux angles du triangle de base r et b, et les deux angles correspondants Hr et Hb du triangle image obtenu par la transformation précisée en remarque préliminaire.
En déplaçant mon point M, je constate que la double égalité des angles (r = Hr & b = Hb) tend à se produire lorsque M est très éloigné du triangle rvb.
Je décide alors de placer M sur la hauteur du triangle rvb relative à v et de l’envoyer à l’infini par l’utilisation d’une animation (ressort). Je constate alors l’égalité des angles pour le passage à l’infini (Figure 1).

Figure 1 (l’infini n’est pas loin !)
Il y a donc trois solutions pour les points à l’infini dans les directions normales aux côtés du triangle rvb.
S’il y a des solutions à l’infini, j’imagine qu’il y a aussi des solutions au voisinage du triangle. Et j’en reviens au cercle circonscrit, pour constater rapidement que son centre est aussi une solution. En effet, les pieds des perpendiculaires menées de M aux côtés du triangle sont alors milieux de ces côtés et les côtés des deux triangles sont alors parallèles deux à deux.
(Figure 2)
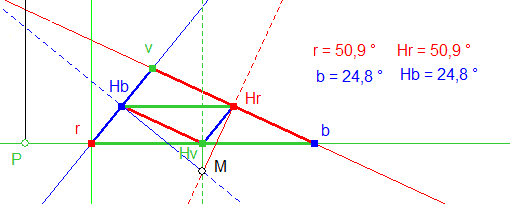
Figure 2
Je vérifie pour terminer que les premières solutions fonctionnent
également pour un point à l’infini dans une direction quelconque
(inverse du centre du cercle circonscrit par rapport à ce cercle).