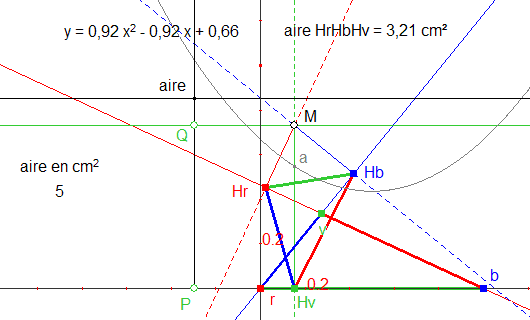
El triángulo inicial es rvb (rojo, verde, azul-bleu).
El estudio del triángulo obtenido tomando los simétricos de un punto M con respecto a los lados rv, vb, br es equivalente al del triángulo correspondiente por una homotecia de centro M y razón ½ : se trata del triángulo construido a partir de los pies Hb, Hr y Hv de las perpendiculares por M a los tres lados rv, vb y br.
Método usado :
El lugar de M cuando el área del triángulo HbHrHv es constante es un círculo de centro en el circuncentro.
A diferencia del primer problema (triángulo rectángulo), es bastante difícil do obtener puntos M por tanteo que determinen un área constante del triángulo HrHvHb.
Así que utilicé el siguiente procedimiento (ver figura 1) :

Figura 1
1. Escojo un número (5) que representa el área en centímetros cuadrados del triángulo (valor variable, a la izquierda de la figura) .
2. Defino un sistema de ejes perpendiculares de origen r z eje x rb.
3. Coloco un punto P sobre el eje de las abscisas, trazo la perpendicular al eje en ese punto y construyo sobre esta una semirrecta de origen P dirigida hacia arriba.
4. Transfiero el área (5) sobre esta semirrecta (punto llamado " aire ") trazo la paralela al eje x por ese punto.
5. Defino un punto Q sobre la recta Paire, trazo la paralela al eje x en ese punto z coloco un punto M sobre esa paralela. Así queda definido un punto M que puedo desplazar en x e y.
6. Mido el área del triángulo HrHvHb y transfiero esa área sobre una semirrecta que pasa por M y de origen en el eje x (punto a).
7. Creo el lugar de a con respecto a M y obtengo una parábola (gris en la figura).
Esta parábola tiene ecuación y = ax^2 + bx + c y sólo c varía cuando M varía…
8. La intersección de la parábola con la recta de ordenada " aire " me permite determinar la posicion de M de manera que el área de HrHbHv sea el valor escogido (5, ver figura 2).
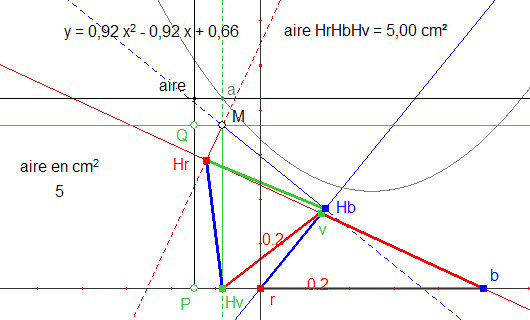
Figura 2
9. Modificando la ordenada de M puedo buscar el lugar de M punto por punto, y encuentro el círculo descrito al comienzo.
10. El archivo aireconstante2.fig (Cabri géomètre II Plus)
muestra una animación.
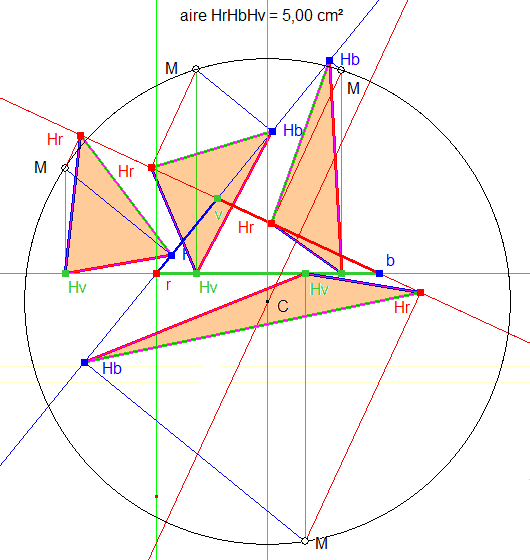
Figura 3
Trazando en Excel las curvas A'=f(r) y A'=g(r) con r radio del círculo
que pasa por M, descubrí que la segunda era la reunión de
dos rectas. Así pude deducir la fórmula del área A'
del triángulo simétrico-lateral cuando el punto describe
un círculo concéntrico con el circuncírculo del triángulo
de referencia
A' = A*abs(1-(r/R)^2)
r : radio del círculo que pasa por M
R : radio del circuncírculo
A : área del tríangulo de referencia.