GeneticGraph

Genetic Algorithm for Aesthetic Graph Layout

Introduction

Graphs are a universally used data structures. They are applied, for example, to represent the interconnections of electronic components, the dependency between software modules, or the hyperlink structure of a Web site. Information structured as a graph is often automatically generated and needs to be communicated to human users in graphical representation. However when its nodes are positioned indiscriminately, a graph generally appears as an incomprehensible mesh of dots and lines. Manually modifying such a mesh as to obtain a more user-friendly result is a difficult and lengthy process as soon as the graph contains more than a few nodes. To be suitable for human interpretation, automatically generated layouts need to comply with some aesthetic rules. However implementing these rules in a computer program can be difficult. Because the problem contain several computational complex sub-problems which in most cases are impossible to solve with systematic methods. Therefore stochastic search methods such as genetic algorithms, are generally used.

Method

A genetic algorithm is a opimization method that imitates the process of natural evolution. A population of potential solutions is maintained and evolved generation after generation towards a designated goal. After each generation, the best individuals are selected and allowed to reproduce whereas the worst individuals are removed from the population. The reproductive process creates new individual based on the genetic code of individuals, selected from the previous generation.
For the problem in question, the individuals subject to genetic optimization are graph layouts. More precisely the positions of the nodes that shape particular layouts are evolved. The individual genes simply contain the x and y-coordinates of the nodes.
The selective fitness is calculated as to be proportional to the visual quality of the layout. The necessary aesthetic criteria are measurable using simple geometry and therefore can be calculated by a computer program. Numerous combinations of aesthetic criteria were tried until satisfactory results were obtained. The final version of the program includes the five following aesthetic criteria:

1. Minimization of the number of edge crossing
2. Minimization of the variance of the edge lengths
3. Maximization of the distance of nodes to the nearest edge
4. Minimization of the variance of the inter-node distance
5. Minimization of the variance of the edge angles at every node

Results

The picture below show a sample layout a graph composed of 18 nodes and 24 edges randomly chosen from the initial population of 500 layouts; it contains 64 edge crossings.

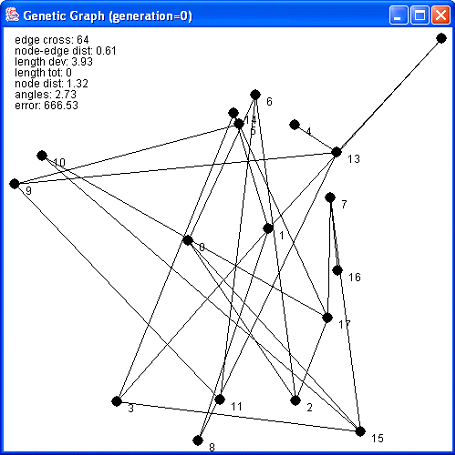
Picture 1: Graph before genetic optimization.

The next picture shows the best layout from the same population as before, after 530 generations. This graph layout is planar; the algorithm was effectively able to find a solution with zero edge crossings. After optimization, the edge lengths display homogeneity and the edge angles are nearly as wide as possible. In addition no node is placed on top of an edge anymore when compared to the previous picture.

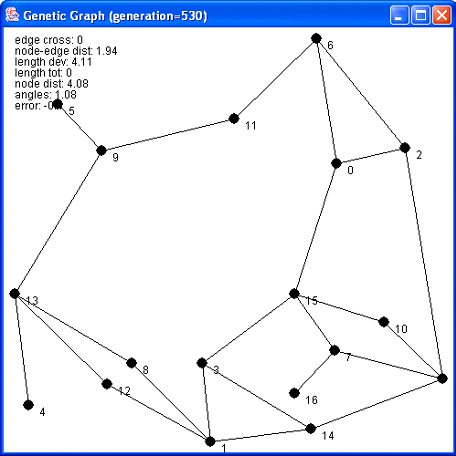
Picture 2: Optimized graph after 530 generations.

In the star graph example below, a central node is connected to 15 other nodes through 15 different edges. The homogenizing effects of the aesthetic criteria are particularly noticeable here. The 15 outer nodes are connected to the central node only and therefore can move relatively freely. The edge angle and inter-node distance criteria result in the nodes being placed at similar angles from each other. The edge length and inter-node distance criteria result in every node being placed at the same distance from the central node, and thus forming a relatively accurate circle.

Picture 3: Star graph.

Conclusion

The genetic algorithm presented here is relatively fast and efficient at suppressing the edge crossings. Most tests that involved planar graphs initially including hundreds of edge crossing where successfully reduced to no crossing at all. However once the edge crossings have been removed, convergence towards a more aesthetic goal is relatively slow. The reason is that if the mutations are relatively efficient at suppressing edge crossings, they are rather poor at performing the fine optimization of the node positions, especially because only one mutation per generation is carried out in each layout.
As an alternative to genetic algorithms, spring algorithms are occasionally used for graph drawing. A spring algorithm is an optimization method where the edges of a graph are considered to be springs pulling together mutually repulsive nodes; it tries to minimize the total tension of the system. At each iteration every node is moved slightly in the direction of the sum vector of all the exerted forces.
In some situations spring algorithms are more efficient than genetic algorithms, especially for fine tuning, however they suffer from some problems too. For example, since the spring algorithm criterion is merely based on reducing tension, there is no rule about avoiding edge crossings. As a result the optimal solution is to use a combination of a genetic algorithm with a spring algorithm, where the genetic algorithm works as the global optimizer and the spring algorithm as the local optimizer.

Yvan Bourquin